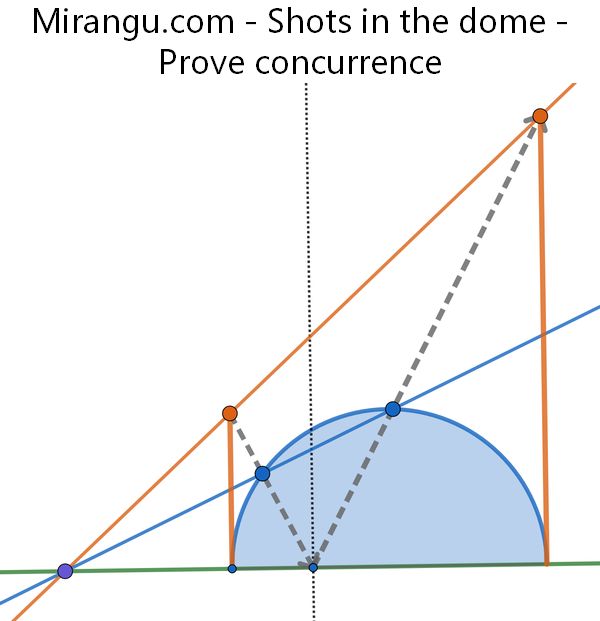
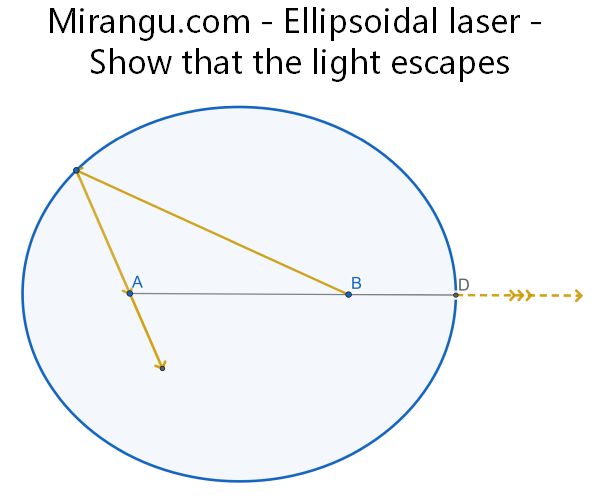
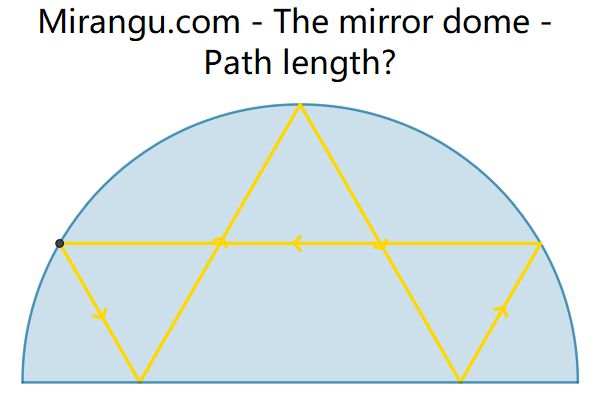
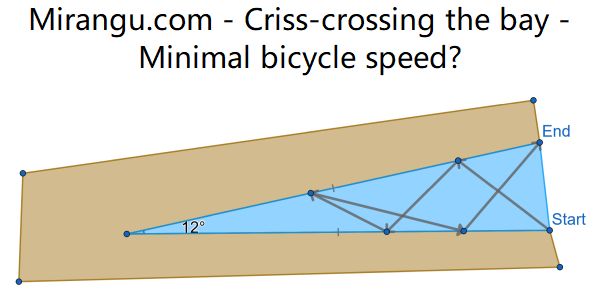
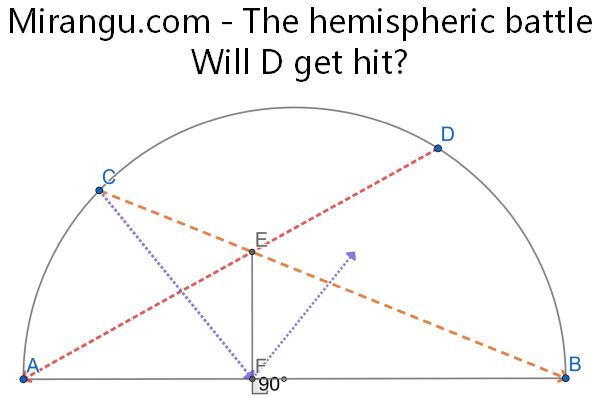
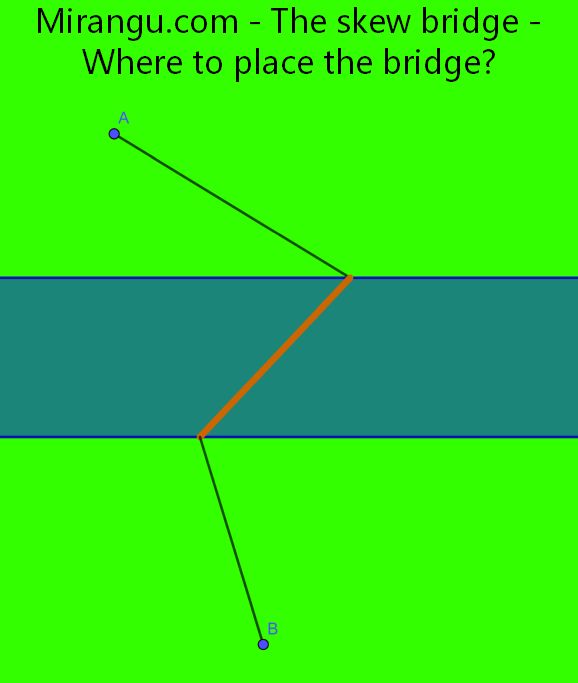
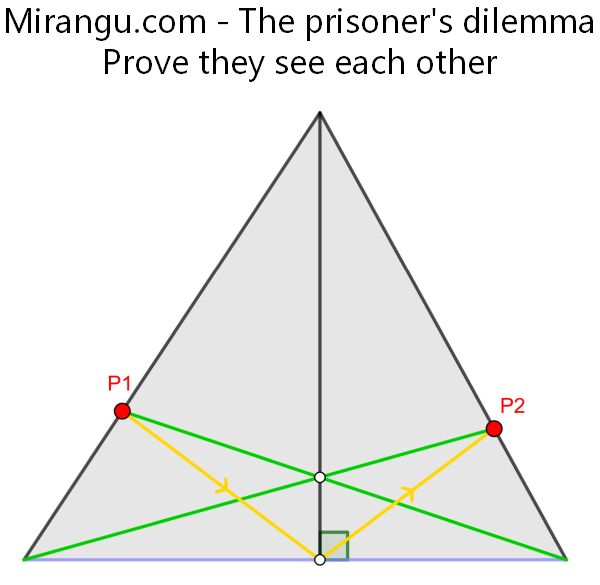
A beam from the top of one tower cuts through the dome, reflects off the ground, and hits the top of the other tower. Show that the line connecting the orange dots, the line connecting the blue dots, and the ground line are concurrent.
Light rays bounce off mirrored walls of a square before reaching one of the other corners. What are the slopes of the light rays leaving A that land in one of the corners B or D after exactly k=5 reflections?
In an equilateral triangular mirror room a laser is shot from the top vertex down to the base. The light ray bounces three times to return to the same base point. What is the angle α?
Three small balloons are in congruent sheds awaiting lift off. The middle shed opens its side flaps. Show that its balloon can inflate, without rolling it, until it is tangent to the sides of the adjacent sheds.
The inside surface of an ellipse is a perfect mirror. There is a pin-hole at an end of the diameter. Show that a light ray emitted from either focus will exit the enclosure via the pin-hole, perhaps after bouncing through the foci several times.
Click for Extra Credit Problems.
A ray of light is emitted from a point on the wall of a mirror-covered semicircle and reflects four times as shown to return to the same spot. If the radius is 1, what is the length of the path?
A boatsman races to cross Isosceles Bay five times, finishing at End. A bicyclist pedals around the bay. How many times faster must the bicyclist travel in order to be sure to beat the boat to End?
C fires at city B and D fires at city A, but their rockets collide in mid-air and fall into the ground at F. Then C fires a laser bouncing off the ground at F at the same angle as incidence. Will the laser beam hit combatant D?
Two points are on opposite sides of a channel. A skew bridge, which has a fixed direction (for instance North East), can be placed anywhere along the channel. Where to place it such that the path from A to B over the bridge is the shortest?
Two prisoners are chained to the walls of a triangular cell. The base is covered with a mirror and a perpendicular wall is separating them. They can each see the opposite corner through a hole. Proof they can see each other through another hole at the base of the perpendicular.
Note that this problem is known as the Blanchet Theorem.