A triangle with sides a, b, c, when extended to whiskers of opposite side length, forms the “Conway Circle”. What is the area of the circle in terms of the expressions a+b+c, ab+bc+ca, abc of the side lengths a, b, c.
Conway circular area
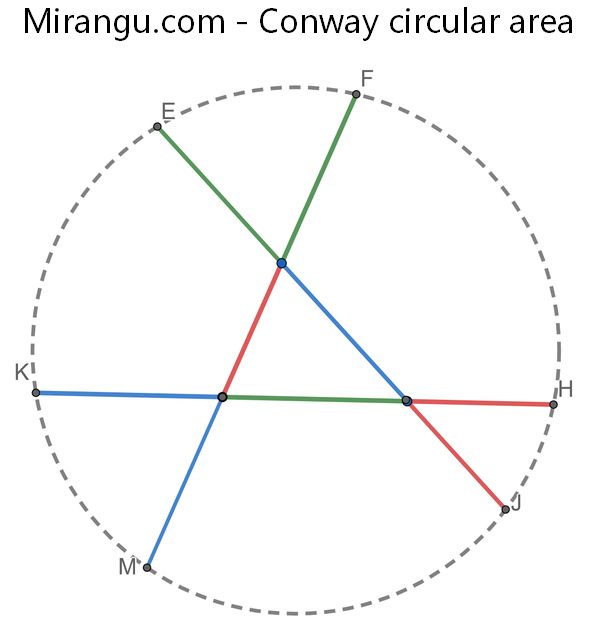

A triangle with sides a, b, c, when extended to whiskers of opposite side length, forms the “Conway Circle”. What is the area of the circle in terms of the expressions a+b+c, ab+bc+ca, abc of the side lengths a, b, c.
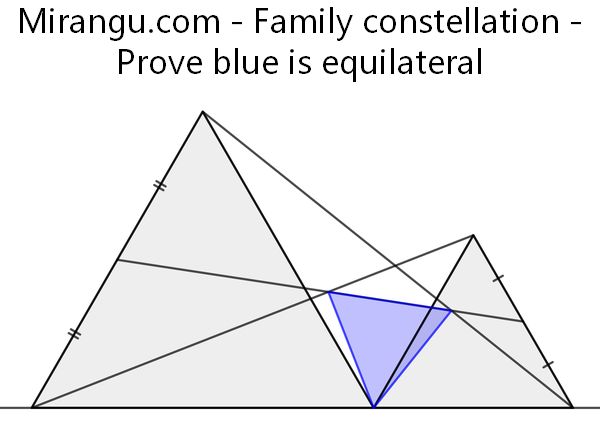
Two equilateral triangles on a line. Prove that the blue triangle is equilateral as well.
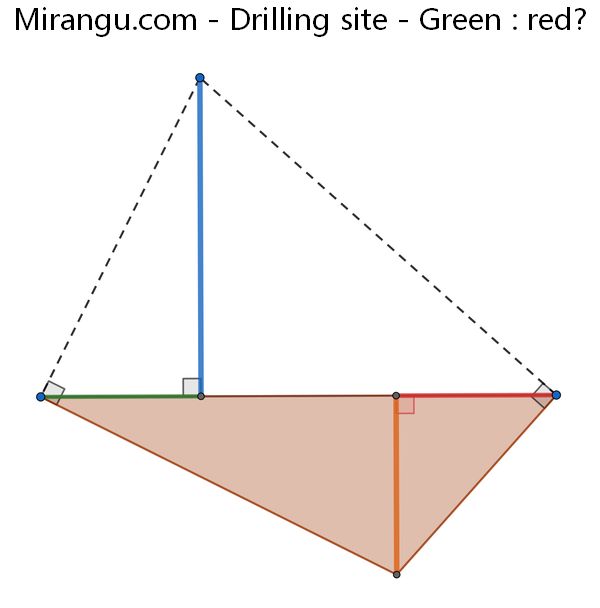
A blue flagpole is erected near a drilling site. Lines are drilled perpendicular to the flagpole guy wires and meet at the bottom of the orange drilling pipe. What is the ratio of distances green to red?
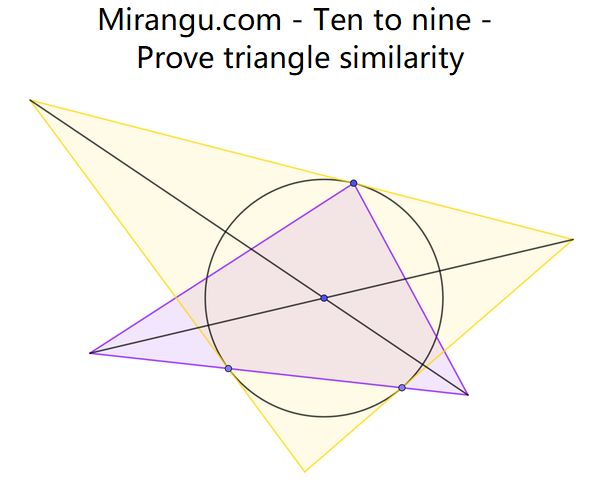
Two triangles and one incircle with its centre and tangency points. Prove that the triangles are similar.
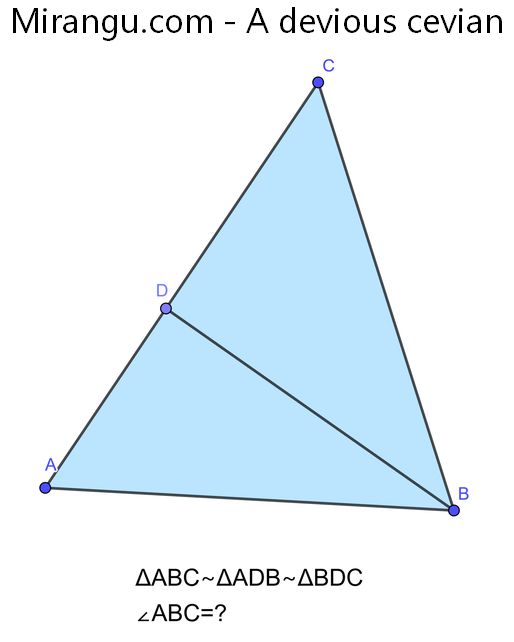
A triangle with a cevian. It is split into two similar triangles. What is angle ABC?
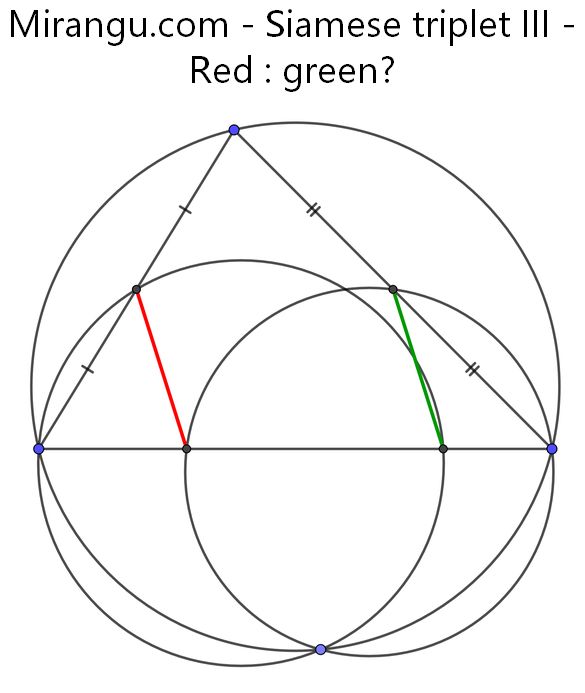
Three circles and a triangle. What is red : green?
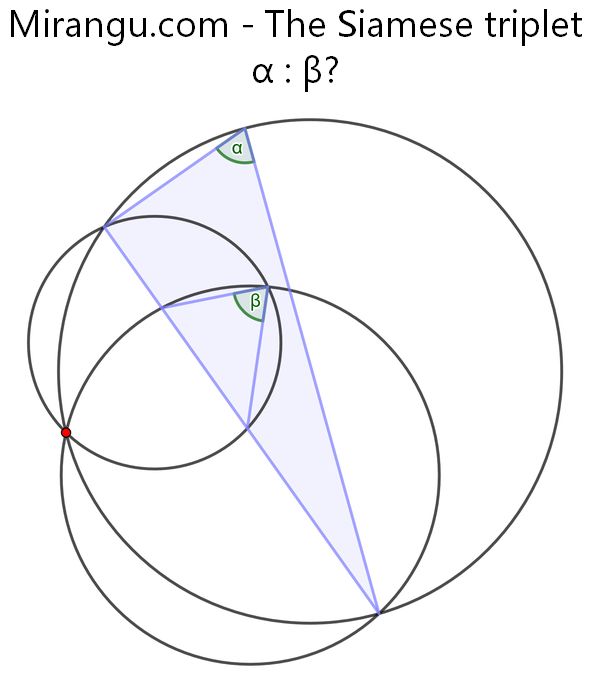
Three circles with a common intersection point and two triangles. What is α : β?
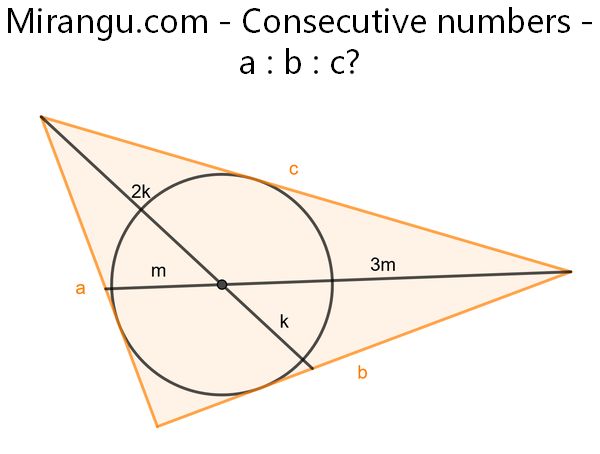
A triangle with its incircle. What’s a : b : c?
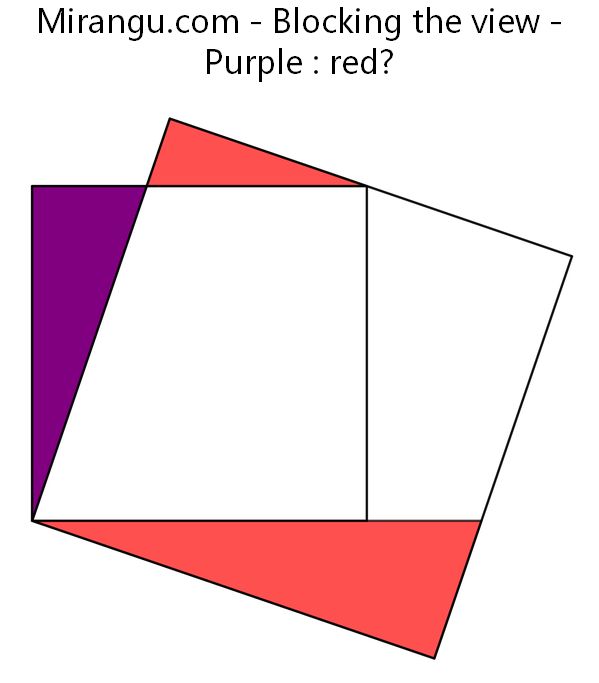
Two squares and one extended side. What is purple : red?
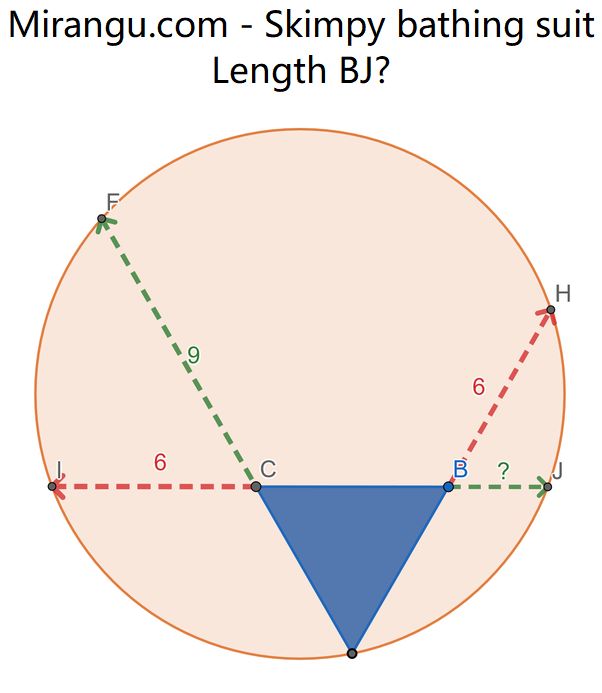
An equilateral triangle with a circle through one vertex, and the intersections FIHJ of the extended sides with the circle. Lengths of three of the external segments are indicated. What is the fourth length?