Two regular pentagons share a vertex. What’s the angle α?
Tipping point II
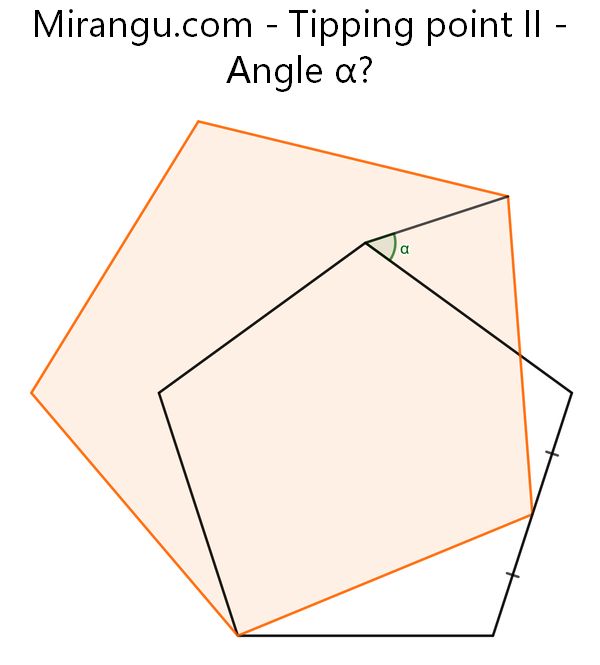

Two regular pentagons share a vertex. What’s the angle α?
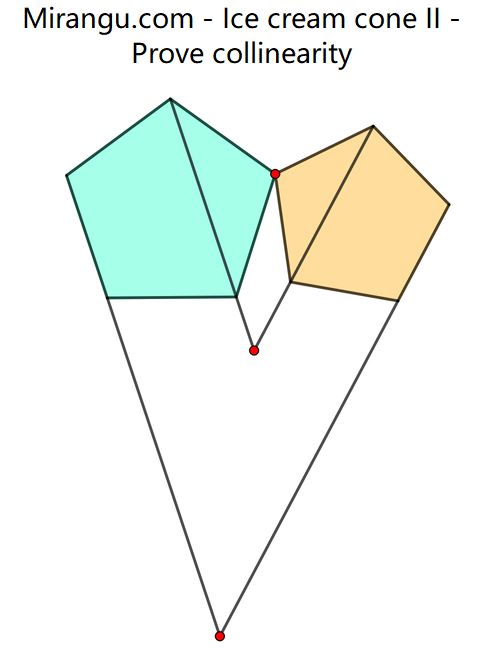
Two regular pentagons sharing a vertex with extended sides and diagonals. Proof that the three red points are collinear.
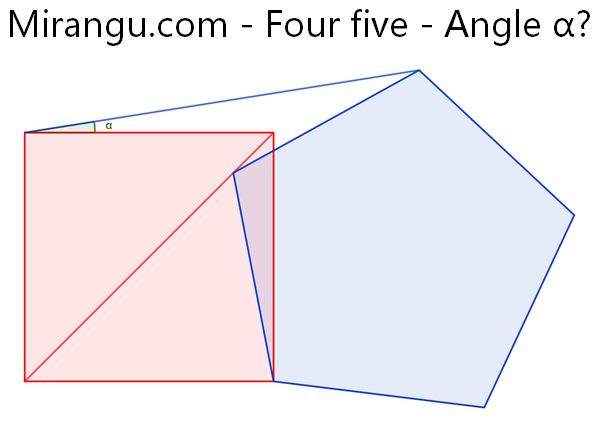
A square and a regular pentagon share a vertex. What’s the angle α?
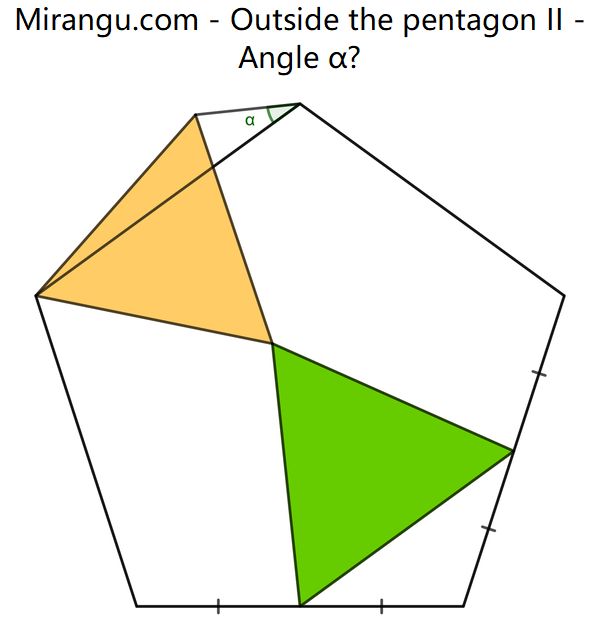
A regular pentagon and two equilateral triangles. What’s the angle α?
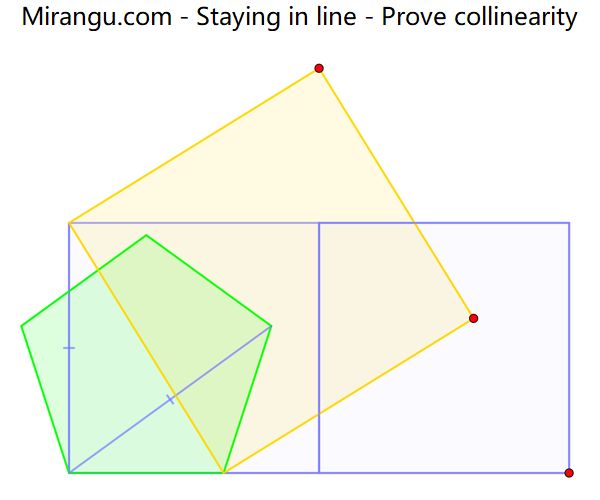
Three squares and a regular pentagon. Prove that the three red vertices are collinear.
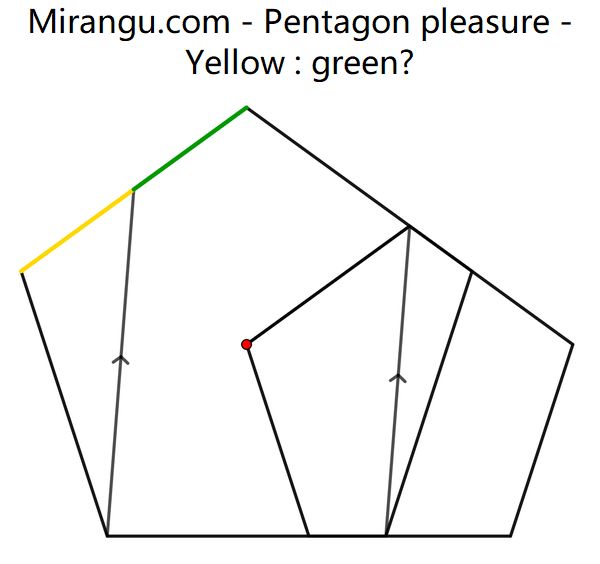
Two regular pentagons. The centre of the large one is a vertex of the small one. What is yellow : green?
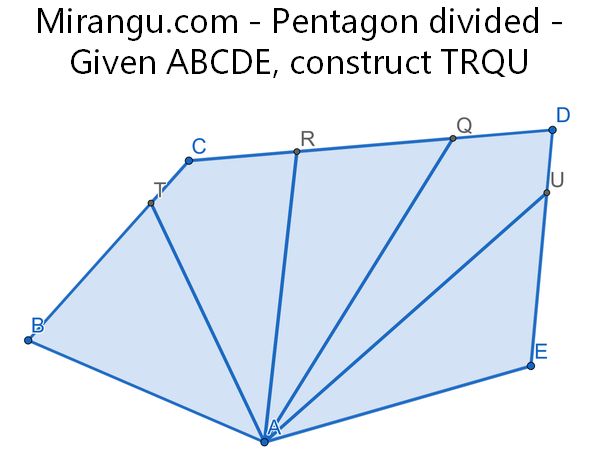
Given a pentagon ABCDE, construct the points T,R,Q,U such that the segments AT, AR, AQ, and AU divide the pentagon into five equal area pieces. (Using straight edge and compass. But you may divide a segment into a number of equal segments for free.)
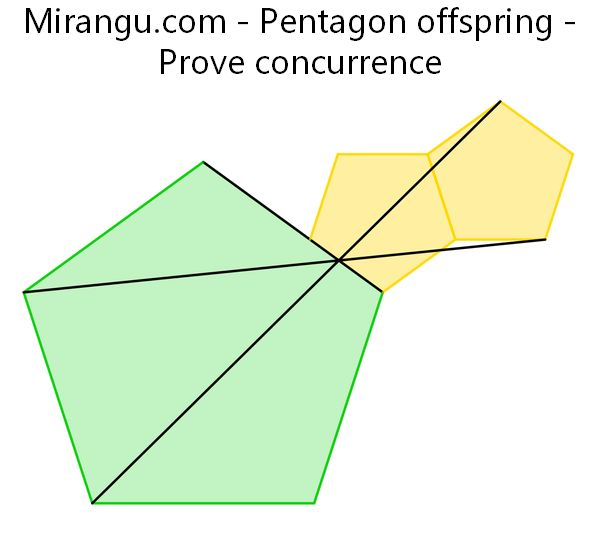
Three regular pentagons are placed as shown. Prove that the three black line segments are concurrent.
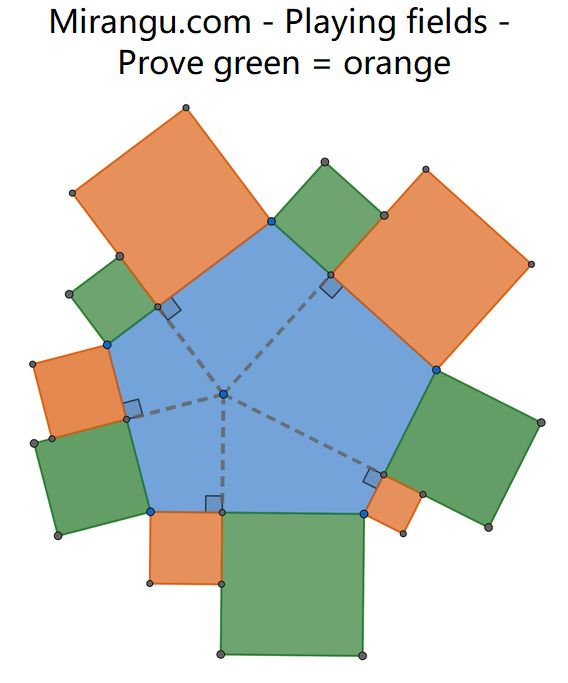
Show equality of the green and orange square playing field areas.
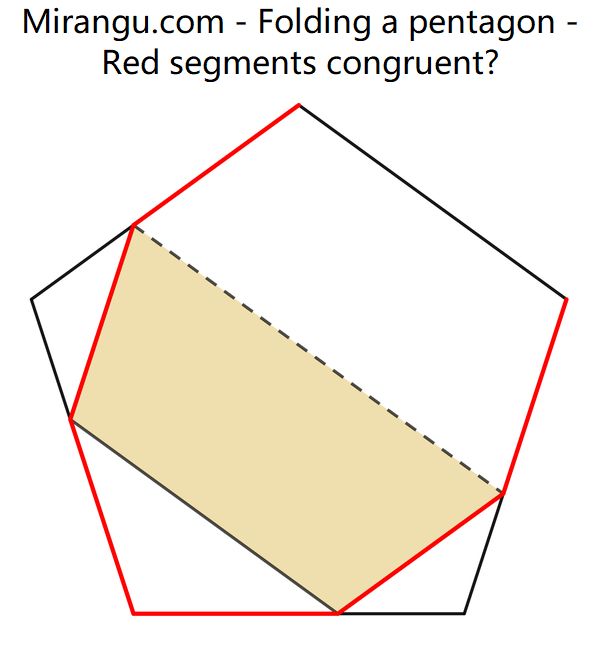
One side of a regular pentagon is folded back and forth as shown. Are the six red line segments congruent?