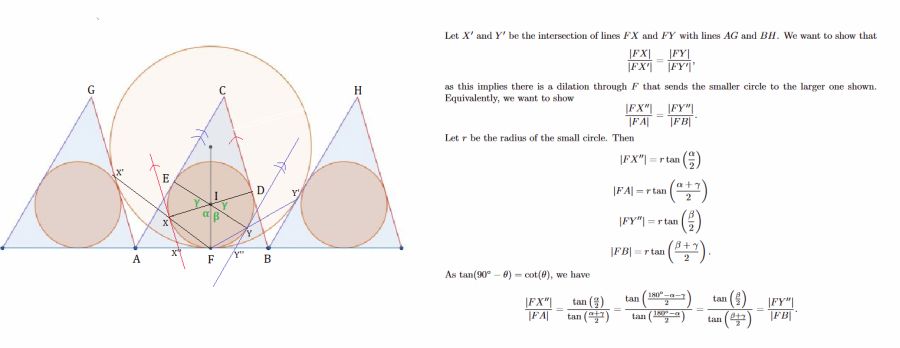
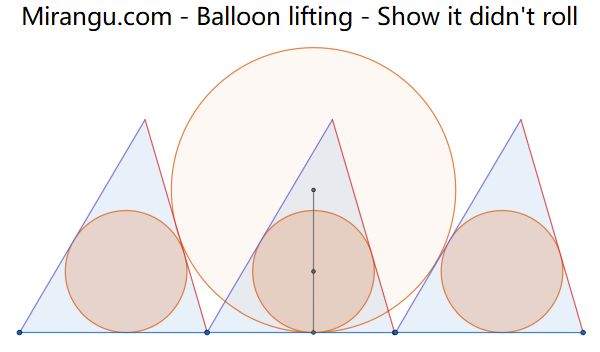
Three small balloons are in congruent sheds awaiting lift off. The middle shed opens its side flaps. Show that its balloon can inflate, without rolling it, until it is tangent to the sides of the adjacent sheds.
Scroll down for a solution to this problem.
Solution
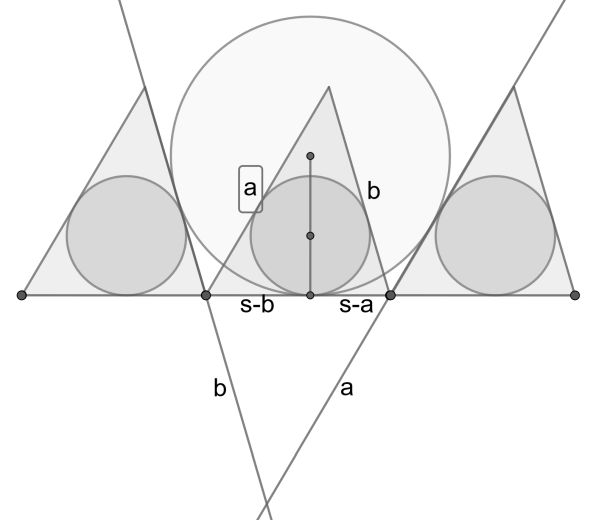
Consider the middle triangle. Using the Incircle Lemma derived in The high-water mark, the distances from the lower vertices to the incircle tangency point are s-b and s-a respectively, where s is the semiperimeter of the triangle.
The trick is to extend the shown sides, so that a congruent triangle is formed below the common base, of which the large circle is an excircle. Now consider the below diagram.
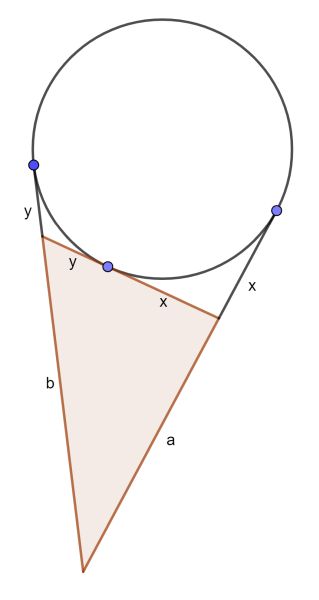
On the one hand we have x+y+a+b=2s, where s is the semiperimeter of the brown triangle. On the other hand we have a+x=b+y. Together this leads to y=s-b and x=s-a.
This shows that the tangency points of the large and middle small circle coincide, implying that the balloon can be inflated without rolling.