A unit square and a rectangle touching three square sides and passing through the midpoint of the upper side. What is the minimal blue area?
Peeping out II
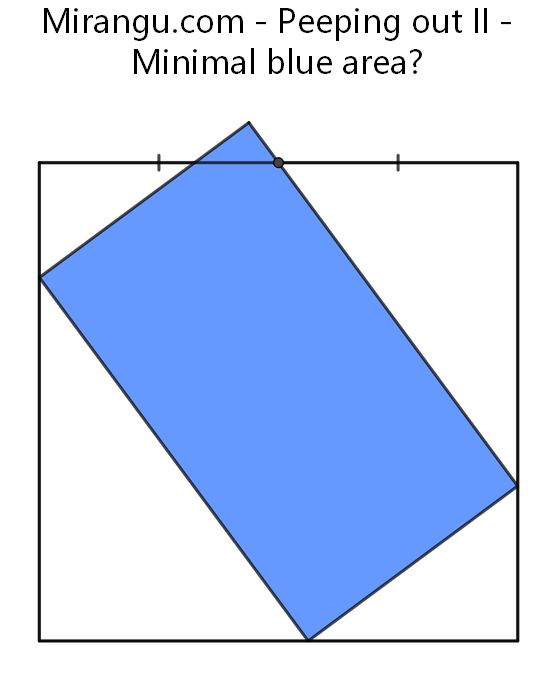

A unit square and a rectangle touching three square sides and passing through the midpoint of the upper side. What is the minimal blue area?
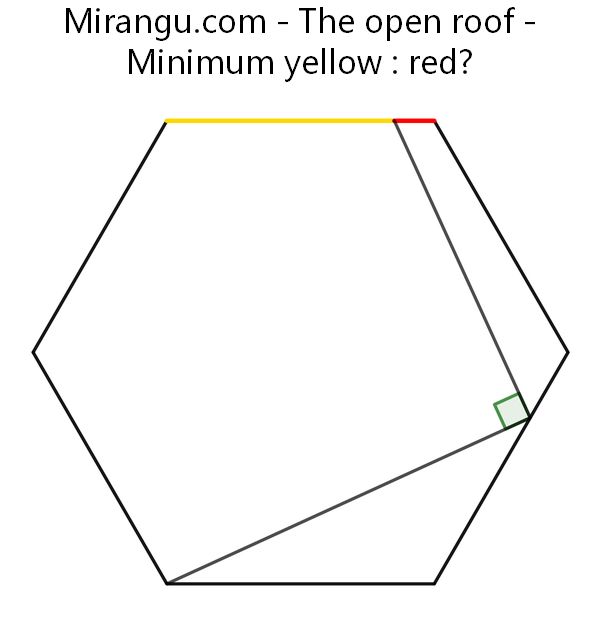
A regular hexagon with two line segments at right angles. What is the minimum of yellow : red?
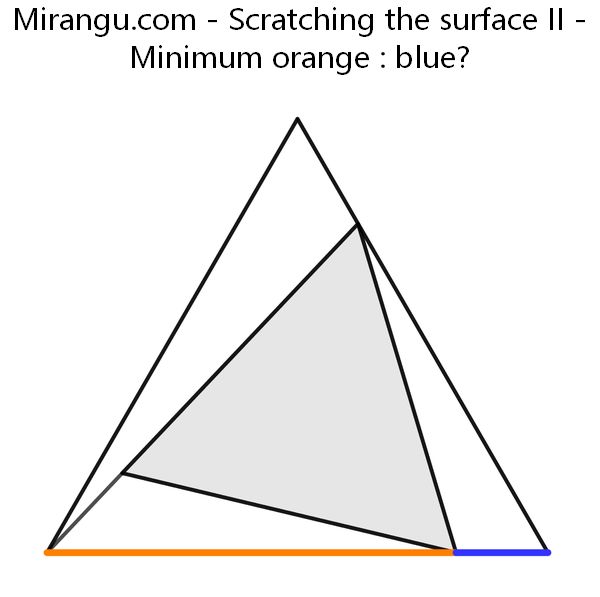
Two equilateral triangles, the smaller one being of variable size. What is the minimum value of orange : blue?
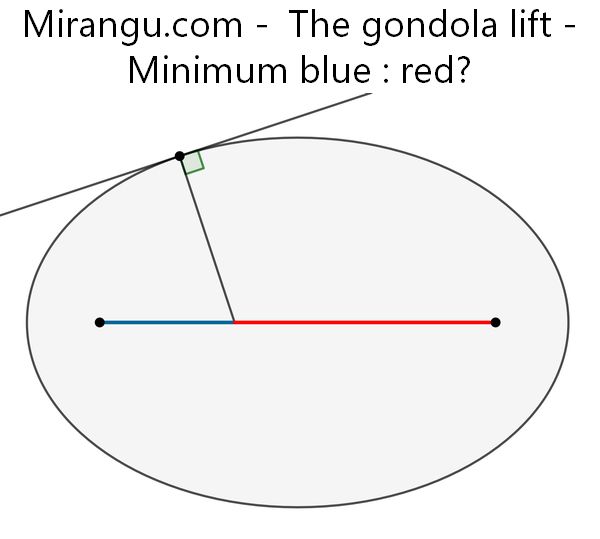
A tangent and its normal in an arbitrary point on an ellipse with eccentricity e. The focal points are also shown. What is the minimum value of blue : red in terms of e?
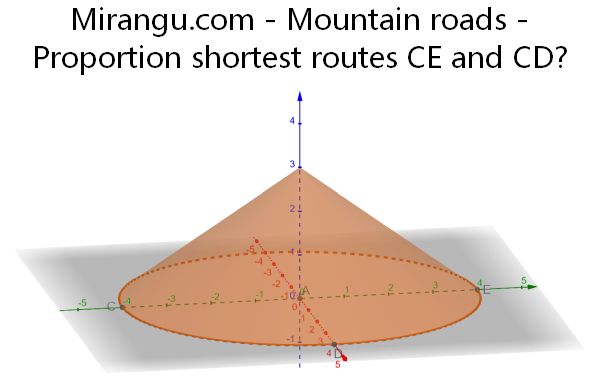
A circular mountain peak has coordinates (0,0,3) and its base has towns C=(-4,0,0), E=( 4,0,0) on opposite sides. Town D=(0,4,0) is halfway between them, around the base. A road goes partially up and down the mountain connecting C and E. Another road connects C and D. Both roads are shortest possible. What is the ratio of the road lengths?
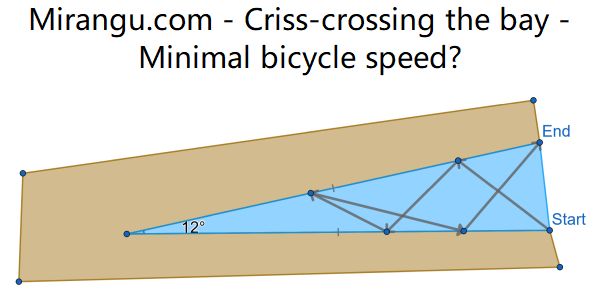
A boatsman races to cross Isosceles Bay five times, finishing at End. A bicyclist pedals around the bay. How many times faster must the bicyclist travel in order to be sure to beat the boat to End?
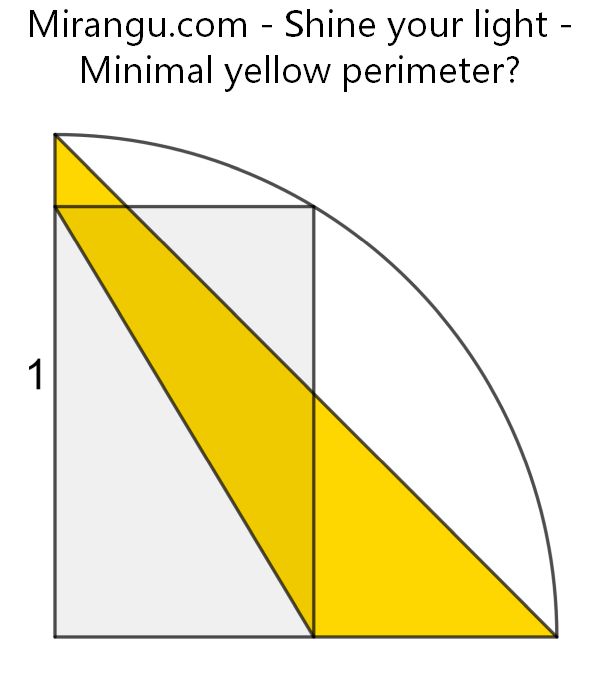
A quarter circle of radius 1, a rectangle touching the circle in an arbitrary point and a yellow quadrilateral. What is the minimal perimeter of this quadrilateral?
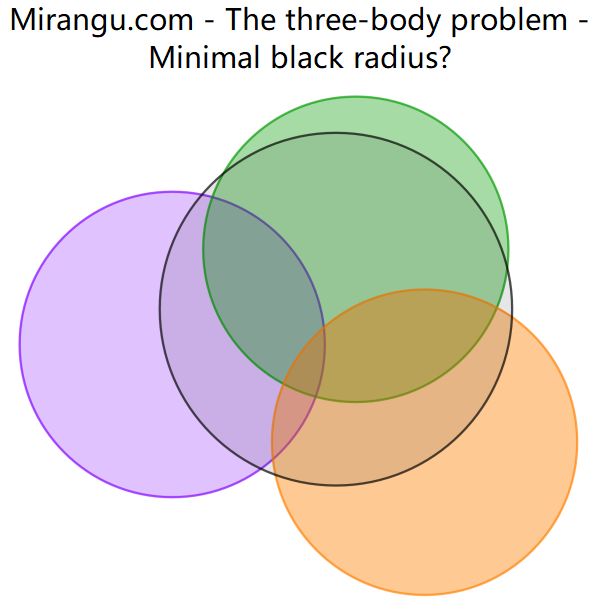
Three coloured unit disks are placed so that they have a common (3-way) intersection, but none of the disks covers the intersection of the other two disks. What is the minimum radius of the disk that would cover all intersections at once, in all cases?
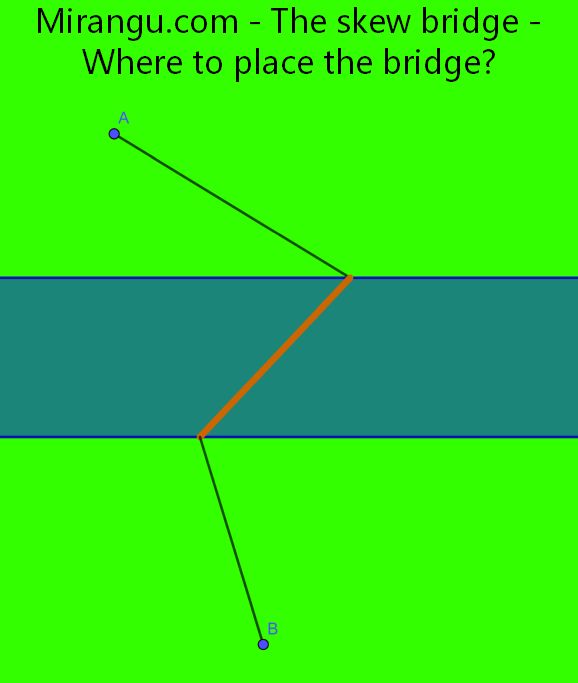
Two points are on opposite sides of a channel. A skew bridge, which has a fixed direction (for instance North East), can be placed anywhere along the channel. Where to place it such that the path from A to B over the bridge is the shortest?
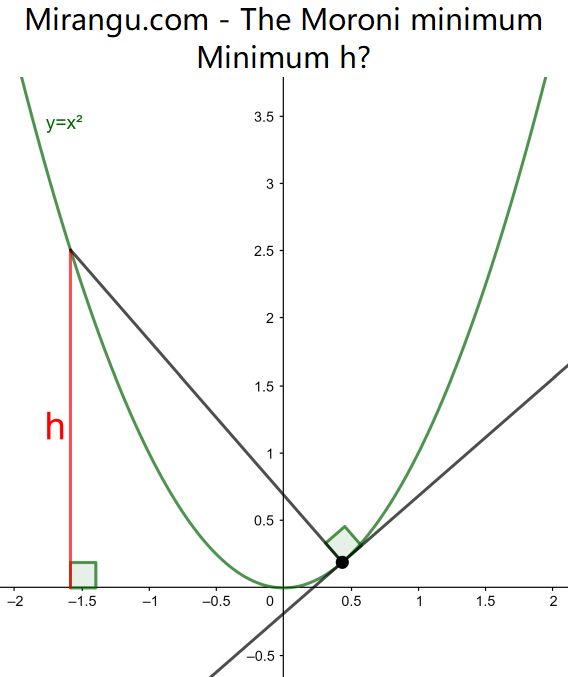
An arbitrary point on the parabola y=x2. Shown are the tangent in that point and a line segment perpendicular to it. What is the minimal height h?