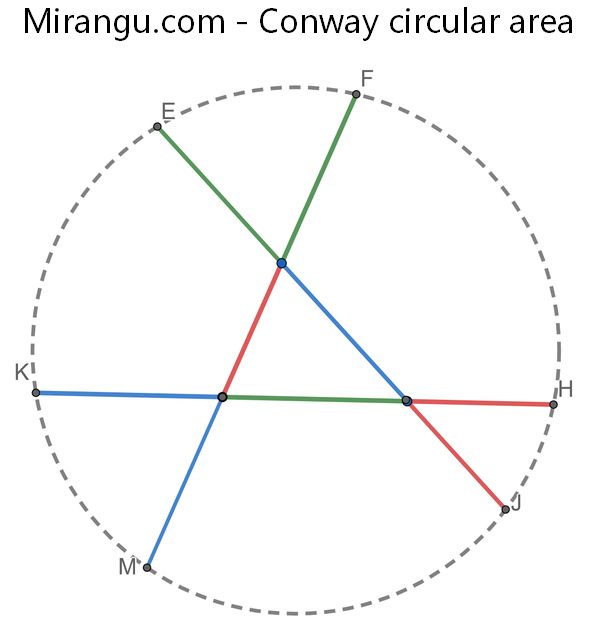
A triangle with sides a, b, c, when extended to whiskers of opposite side length, forms the “Conway Circle”. What is the area of the circle in terms of the expressions a+b+c, ab+bc+ca, abc of the side lengths a, b, c.
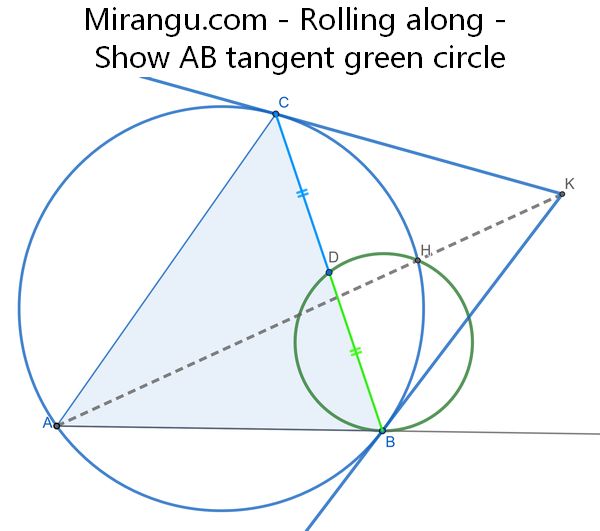
Tangents to the blue circle (ABC) intersect at a point K, and the line AK intersects (ABC) at H. D is the midpoint of BC. Show that the green circle (DHB) is tangent to the line AB.
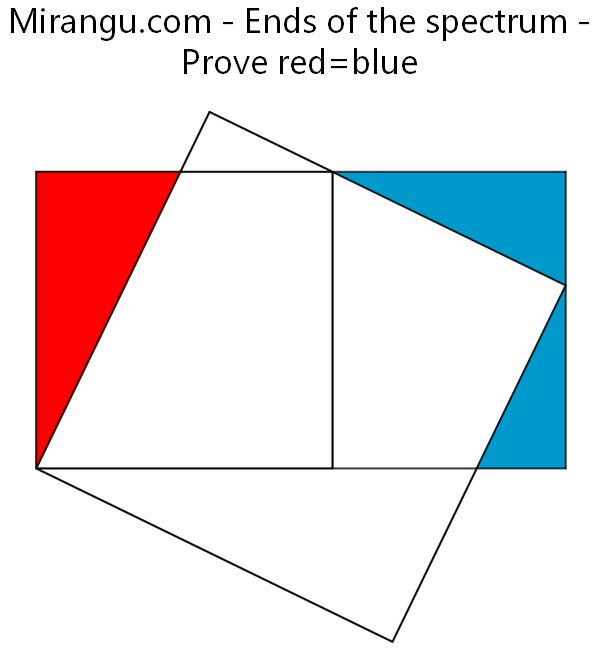
Two squares and a rectangle. Prove that red = blue.
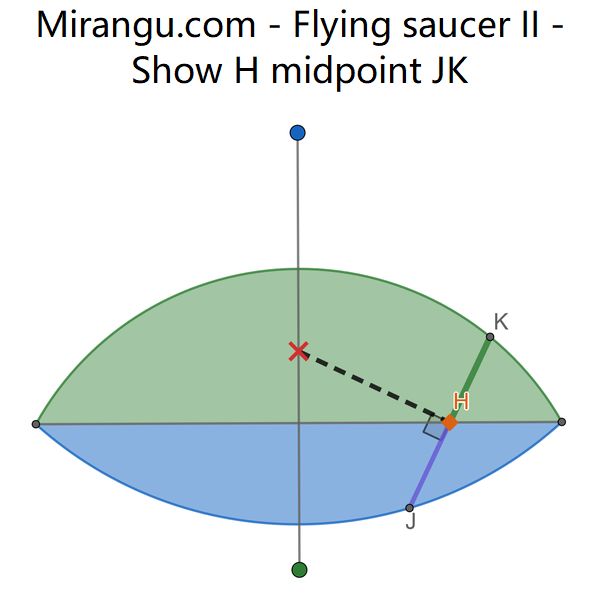
If X is the midpoint of the segment connecting the centers of the upper and lower arcs, and JK is perpendicular to XH, then show that H is the midpoint of JK.
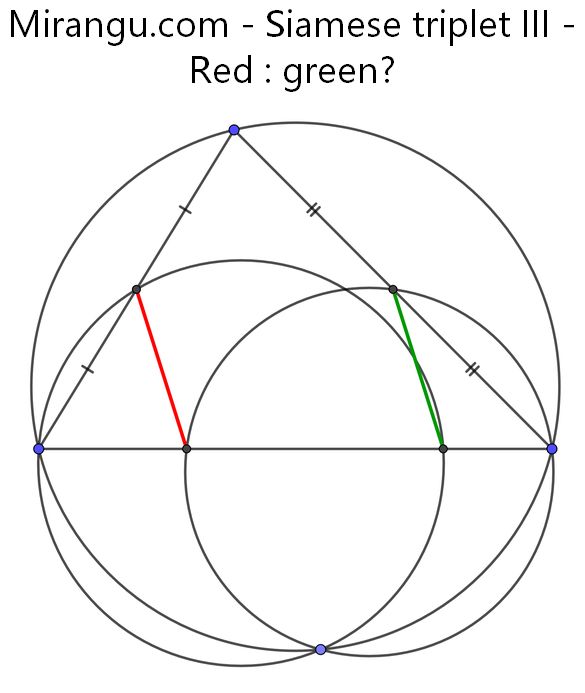
Three circles and a triangle. What is red : green?
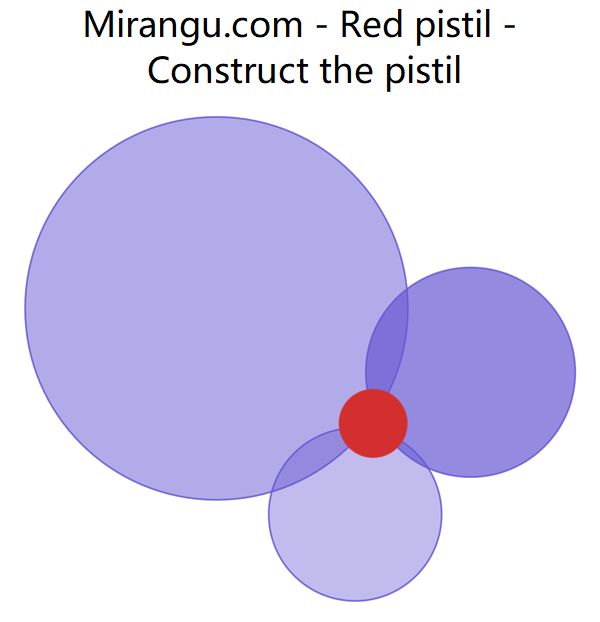
Three circular petals surround a red pistil which is orthogonal to each of the petals. Given the petals, construct the pistil. (You may assume that you are given a direct way to construct a tangent line from an exterior point to any circle.)
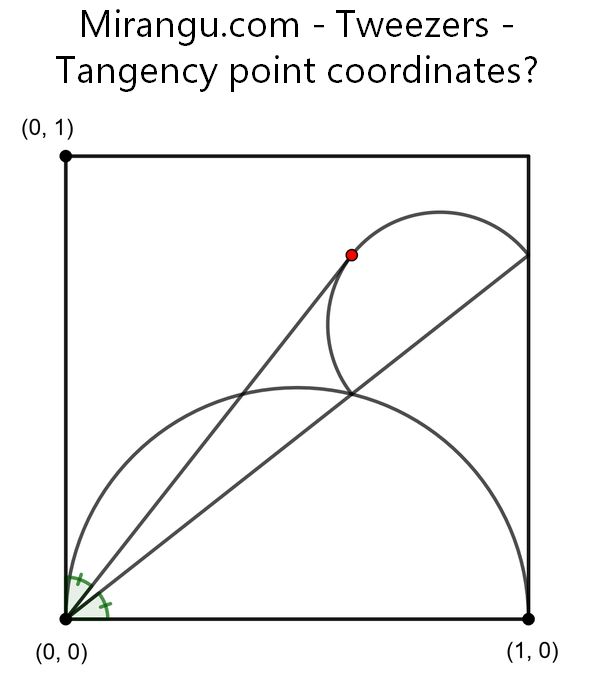
A square with two semicircles. The smaller one has an extended diameter and a tangent. What are the coordinates of the tangency point?
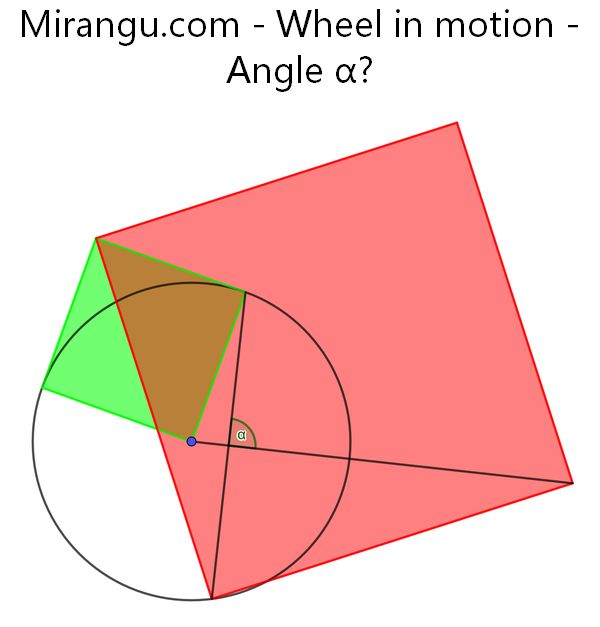
A circle with its centre and two squares sharing a vertex. What’s the angle α?
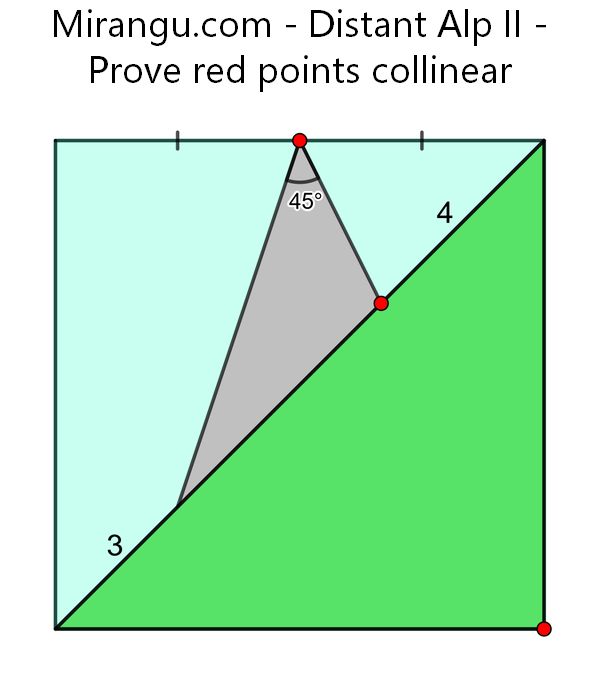
A square with its diagonal. Prove that the three red points are collinear.
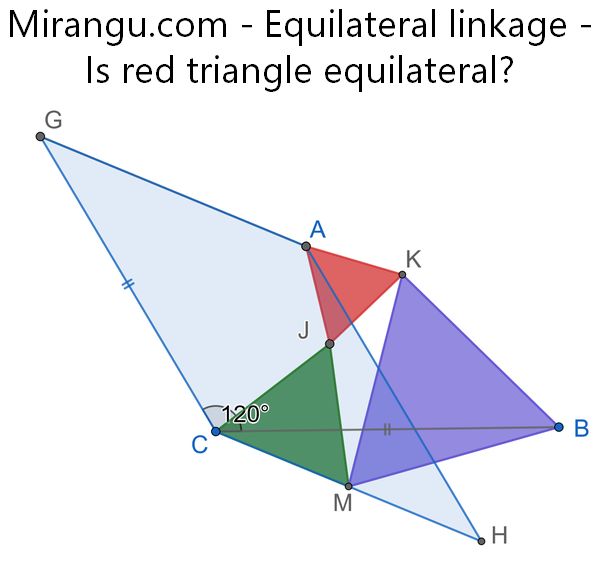
Given 3 points A, B, C, define G so CG=CB and angle GCB is 120 degrees. Define M as the midpoint of side CH of the parallelogram CGAH. The green equilateral has side CM and the purple equilateral has side MB. Is AJK also equilateral?