Categories
Categories
Conway circular area
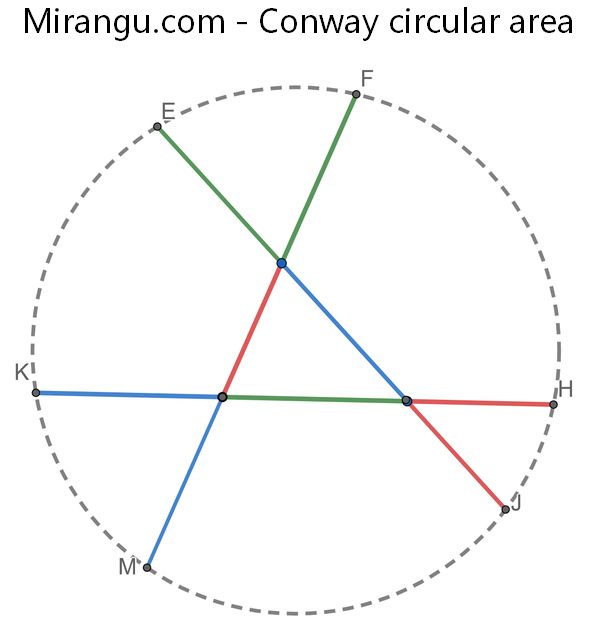
A triangle with sides a, b, c, when extended to whiskers of opposite side length, forms the “Conway Circle”. What is the area of the circle in terms of the expressions a+b+c, ab+bc+ca, abc of the side lengths a, b, c.
Categories
Family constellation
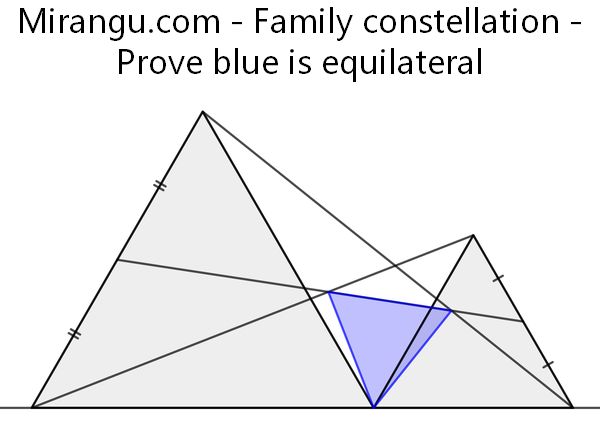
Two equilateral triangles on a line. Prove that the blue triangle is equilateral as well.
Categories
Video: Quad stretches
Categories
Tipping point II
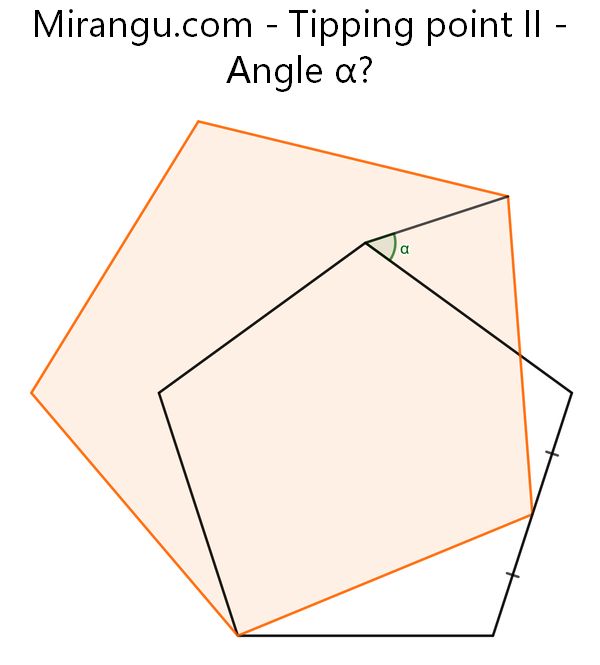
Two regular pentagons share a vertex. What’s the angle α?
Categories
All connected
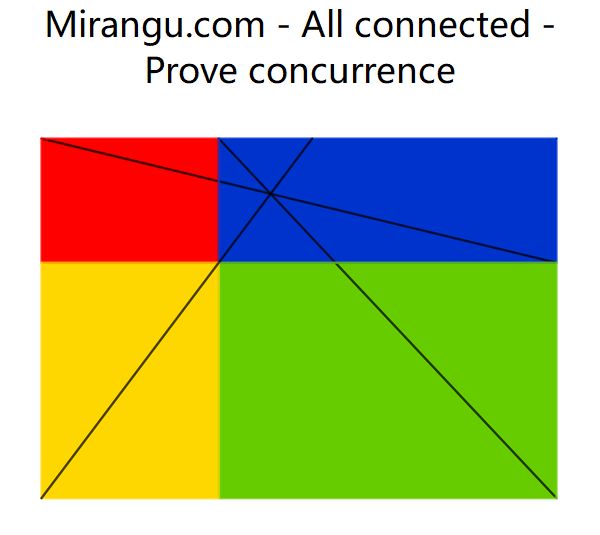
Four coloured rectangles and three line segments. Prove that the three line segments are concurrent.
Categories
Video: A devious cevian
Categories
Drilling site
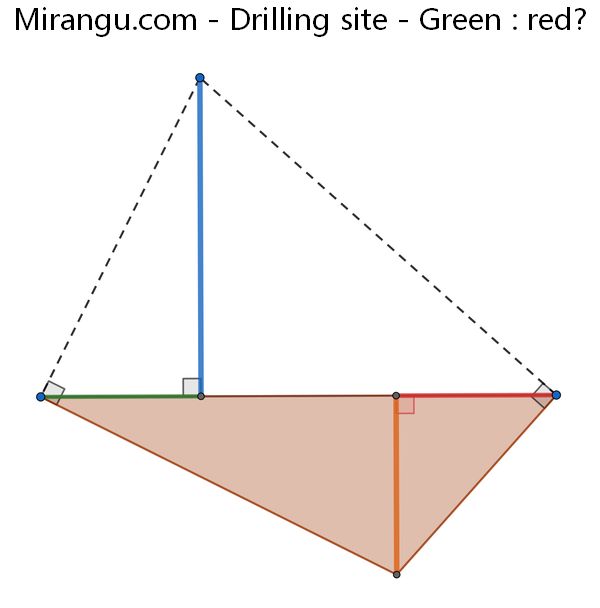
A blue flagpole is erected near a drilling site. Lines are drilled perpendicular to the flagpole guy wires and meet at the bottom of the orange drilling pipe. What is the ratio of distances green to red?
Categories
Video: Ends of the spectrum
Categories
Rolling along
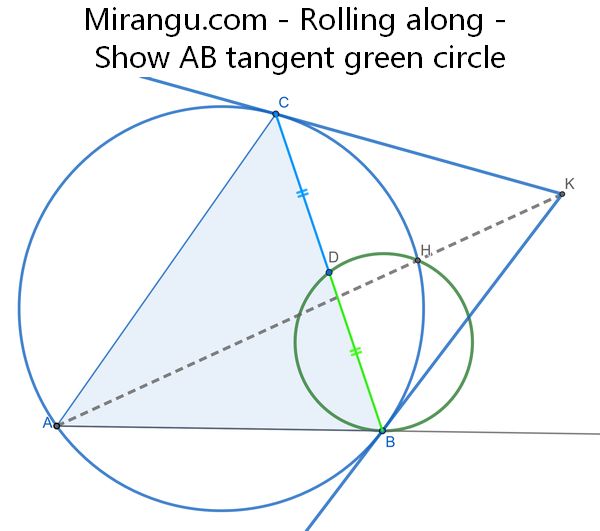
Tangents to the blue circle (ABC) intersect at a point K, and the line AK intersects (ABC) at H. D is the midpoint of BC. Show that the green circle (DHB) is tangent to the line AB.