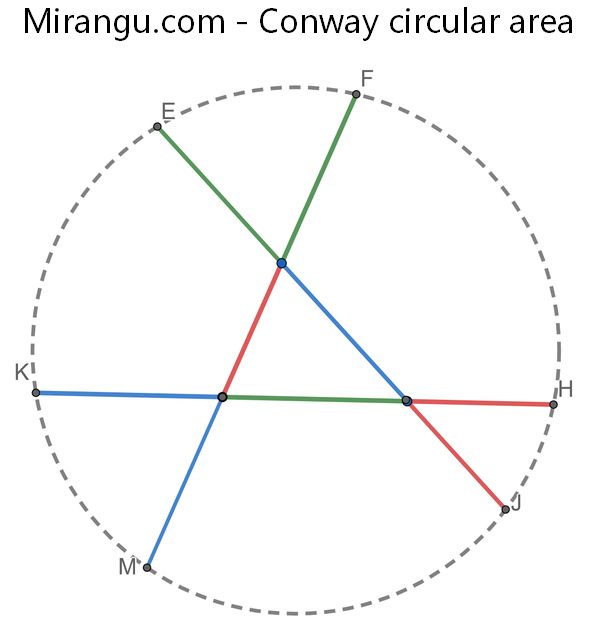
A triangle with sides a, b, c, when extended to whiskers of opposite side length, forms the “Conway Circle”. What is the area of the circle in terms of the expressions a+b+c, ab+bc+ca, abc of the side lengths a, b, c.
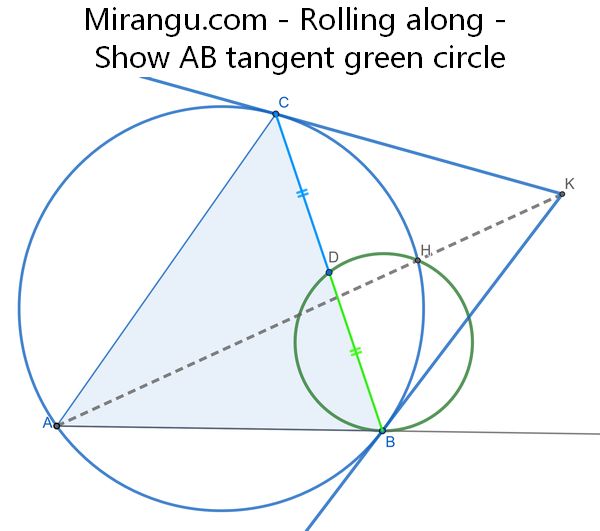
Tangents to the blue circle (ABC) intersect at a point K, and the line AK intersects (ABC) at H. D is the midpoint of BC. Show that the green circle (DHB) is tangent to the line AB.
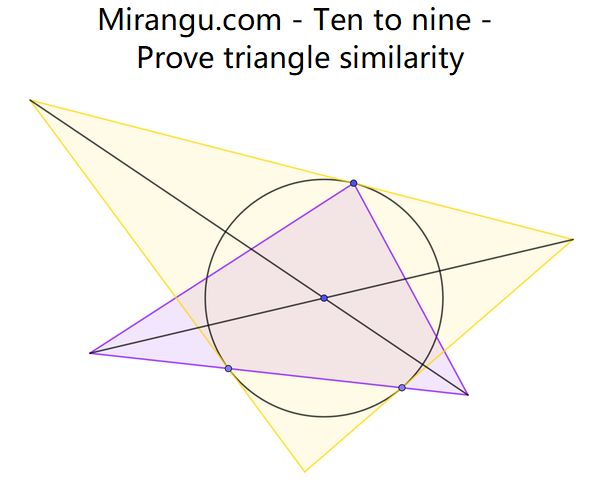
Two triangles and one incircle with its centre and tangency points. Prove that the triangles are similar.
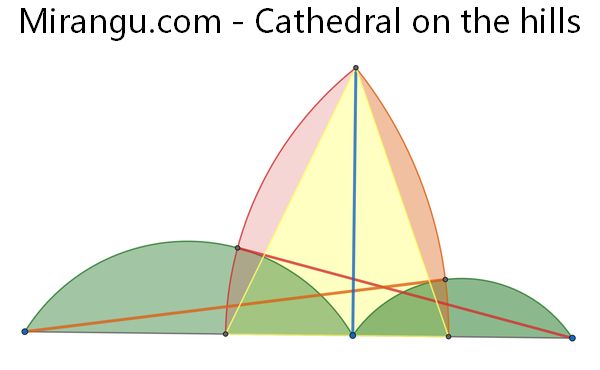
A cathedral is erected on two hills, the side circular arcs whose centers are the hill ends, and so that the right (and left) side arcs are orthogonal. Show that the tip of the spire is directly above where the hills meet.
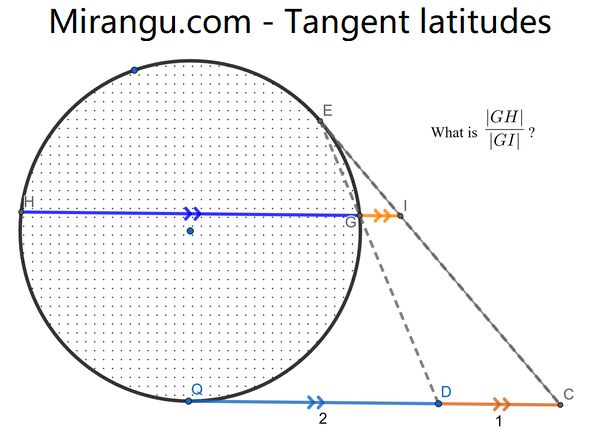
Tangent lines QC and EC meet at C. A point D on QC has DC=1 and QD=2. The line ED intersects the circle at G, and the line HGI is parallel to QDC. What is HG/GI?
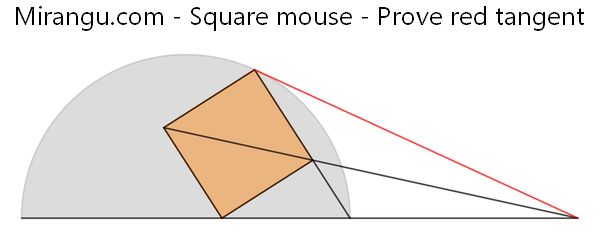
A semicircle and a square with extended side and diagonal. Prove that the red line segment is tangent to the semicircle.
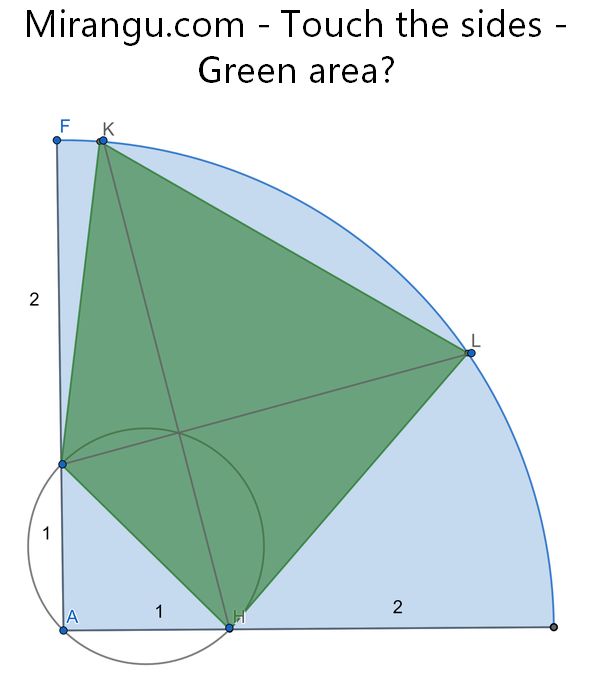
What is the area of a green quadrilateral that fits inside a quarter circle, and has perpendicular diagonals?
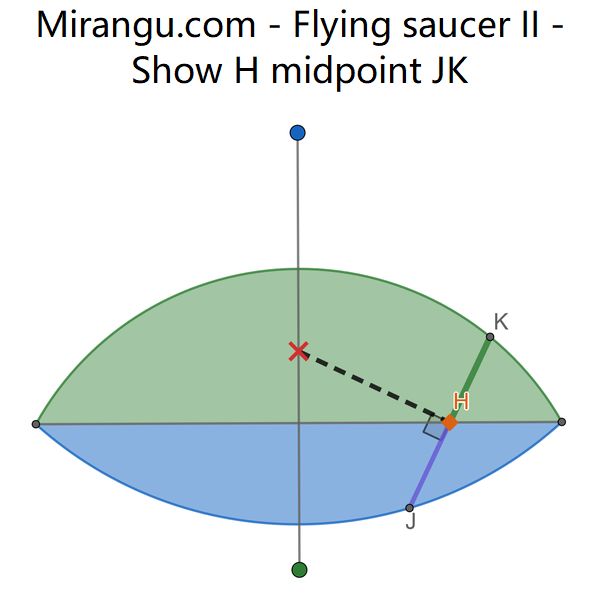
If X is the midpoint of the segment connecting the centers of the upper and lower arcs, and JK is perpendicular to XH, then show that H is the midpoint of JK.
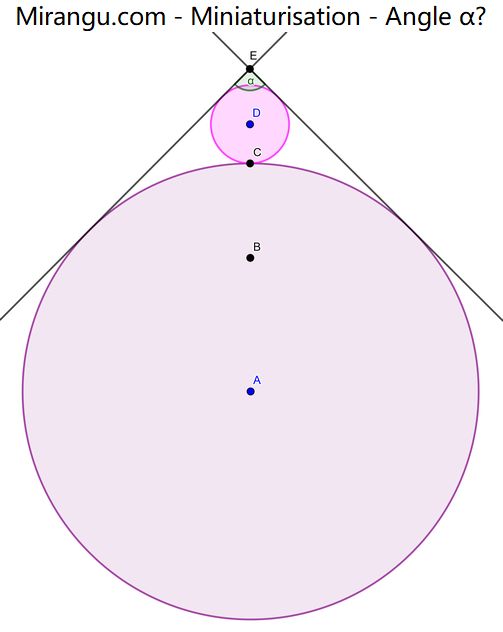
Two tangent circles and two common tangents. A and D are centres. B is midpoint of AD. C is midpoint of BE. What is the angle α?
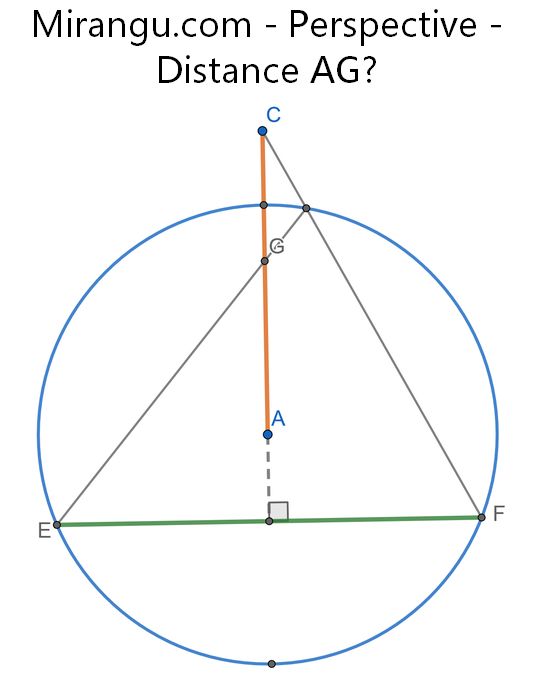
A is the center of a unit circle. What is the distance AG if the distance AC = x?