Four squares are placed as shown. Prove that the green quadrilateral is a parallelogram.
Categories
Stretch of imagination
Tag: parallelogram
Categories
Ace of diamonds II
A parallelogram is inscribed in a quadrilateral. What fraction is red?
Categories
Monolith among the moons
The points of intersection of the purple and green circles line up with the points of intersection of the green and orange, lines meeting on the orange circle. Show that the circle centers plus the orange point form a parallelogram.
Categories
Sloppy clothes
Green and blue tangent circles, with centers A, D. Parallelogram ADCB, with C on the edge of the green. Red semicircle on diameter AC. Dotted circle through C with center B. Show that the green, red, and dotted arcs have a common point.
Categories
Circular cuts
The blue parallelogram’s vertex C lies on a green circle that intersects the diagonal BC at J. What is the length of the red segment?
Categories
The fountain plaza
The incircle of ABC touches sides at I and J. D, E, F are the bases of altitudes from C, B, and A. The incenters of BDF of CEF are N and M, respectively. Show that JIMN is a parallelogram and that IM is perpendicular to BC.
Categories
Equilateral linkage
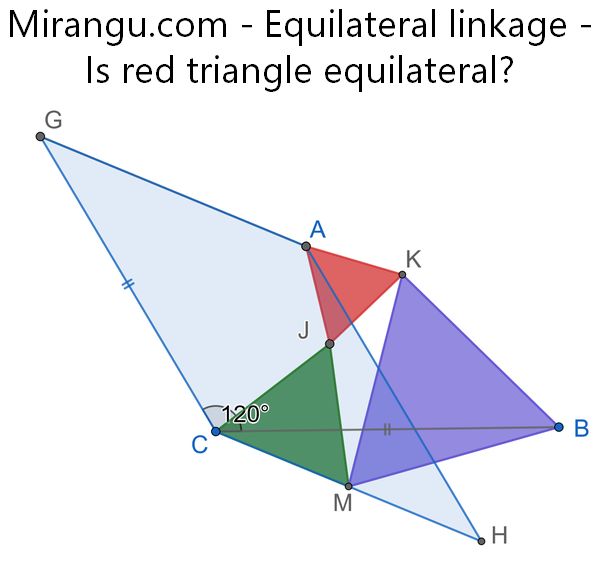
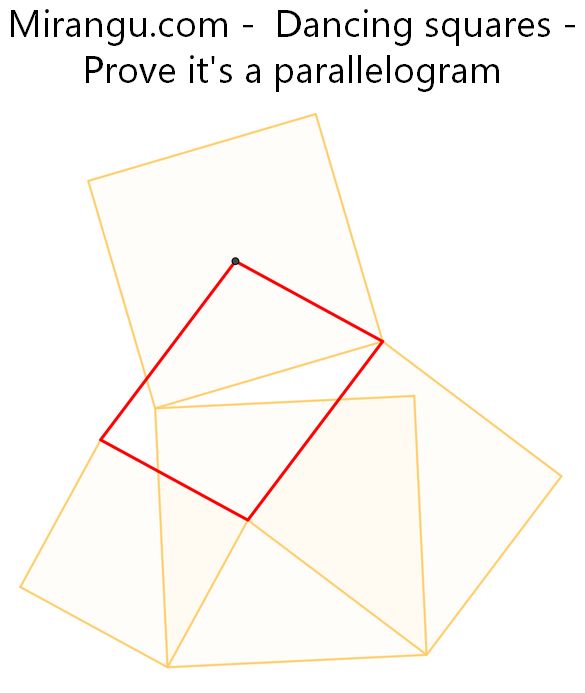
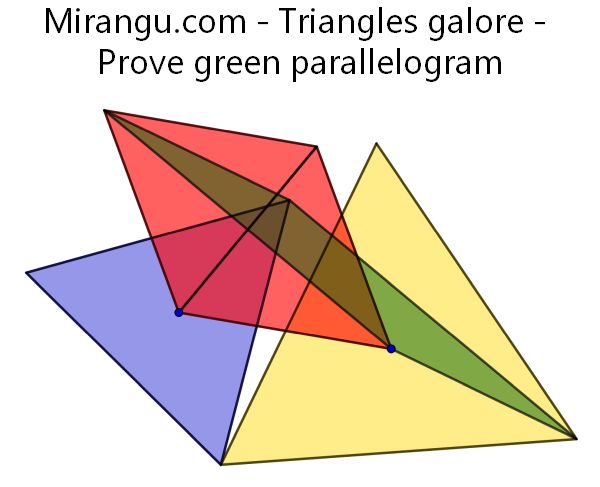
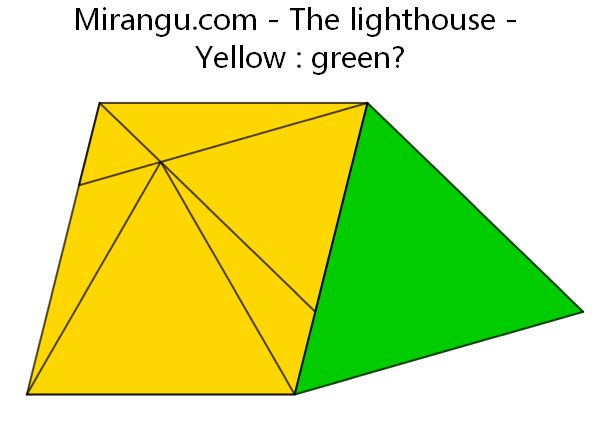
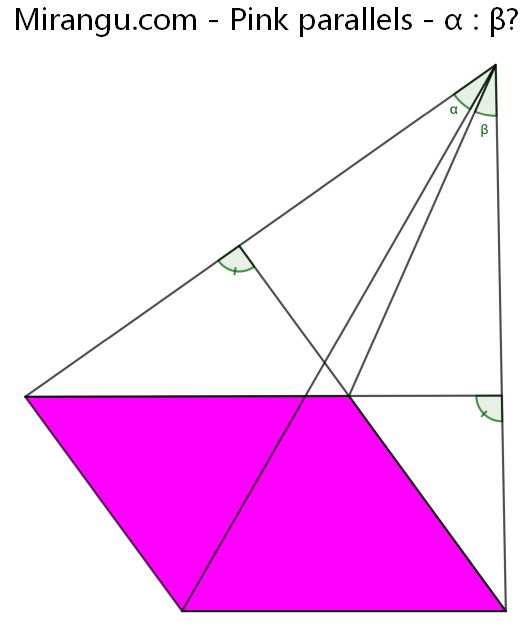
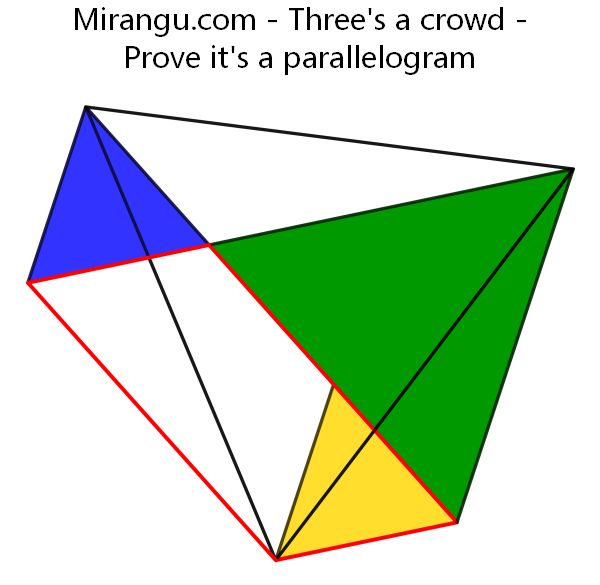
Given 3 points A, B, C, define G so CG=CB and angle GCB is 120 degrees. Define M as the midpoint of side CH of the parallelogram CGAH. The green equilateral has side CM and the purple equilateral has side MB. Is AJK also equilateral?
Categories
Hidden parallelogram
Blue circle (ACDGB) with CEG || AB. Pink circle (EDG) intersects AB at I. Extend DI to intersect blue circle at J, then JC intersects AB at M. Show that IM = CE.
Categories
The square sail
A quadrilateral and a parallelogram share two sides, and a vertex from each determine the orange square. The lengths BC, EF, AD are 4,5,7 respectively, where E and F are midpoints of AB and DC. What is the orange area?
Categories
Euclid’s wing
Several line segments, some of which are parallel. What is green : orange?