An ellipse with its focal points, major and minor axis. What is x, the distance from the centre to the right focal point?
Categories
Egg of Columbus
Tag: ellipse
Categories
A good egg
An ellipse with its focal points and a tangent line. What is the angle α?
Categories
Pumpkin tracing
The point E moves along the outer circle whose center is G. Points A and B are fixed, whereas F and B’ vary with E. Show that F traces an ellipse as E moves along the outer circle.
Categories
The gondola lift
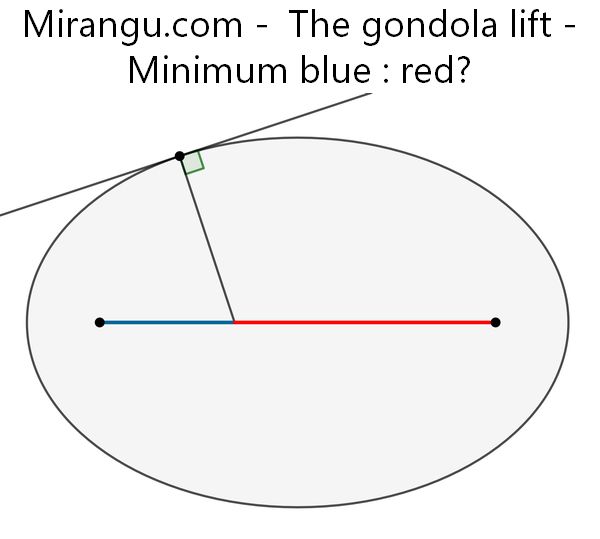
A tangent and its normal in an arbitrary point on an ellipse with eccentricity e. The focal points are also shown. What is the minimum value of blue : red in terms of e?
Categories
Ellipsoidal laser
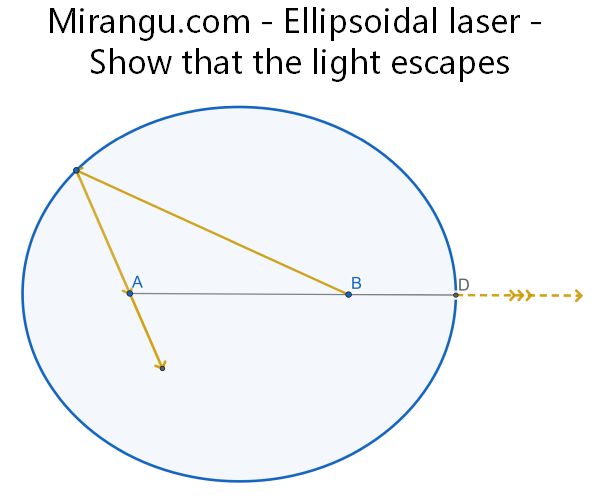
The inside surface of an ellipse is a perfect mirror. There is a pin-hole at an end of the diameter. Show that a light ray emitted from either focus will exit the enclosure via the pin-hole, perhaps after bouncing through the foci several times.
Click for Extra Credit Problems.
Categories
The lorgnette
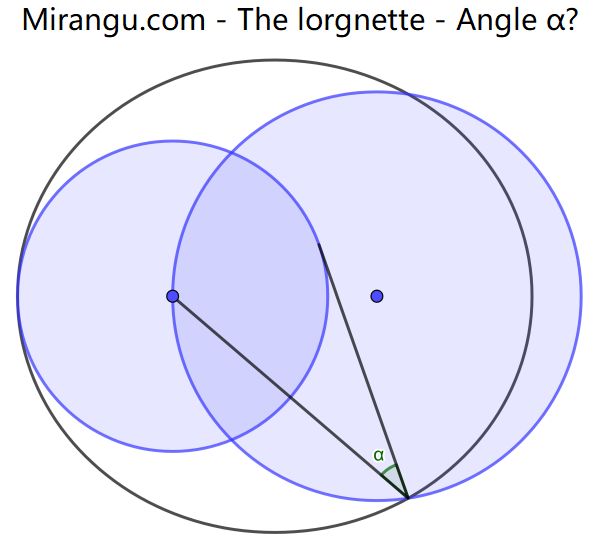
An ellipse, two circles centred in its focal points, a chord and a tangent. What is the angle α?
Categories
Pushing the boundary
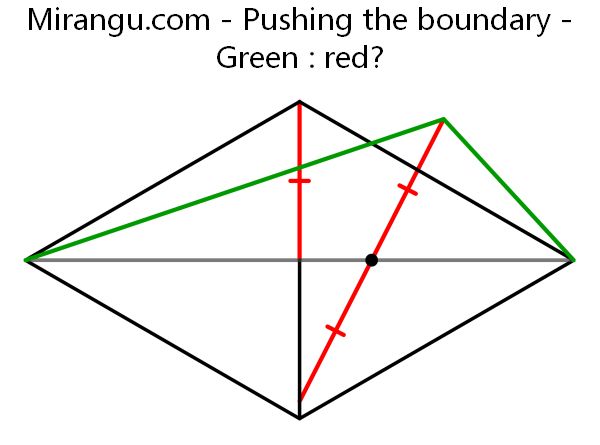
Two equilateral triangles are placed side by side. What’s the proportion green : red?
Categories
The gyroscope
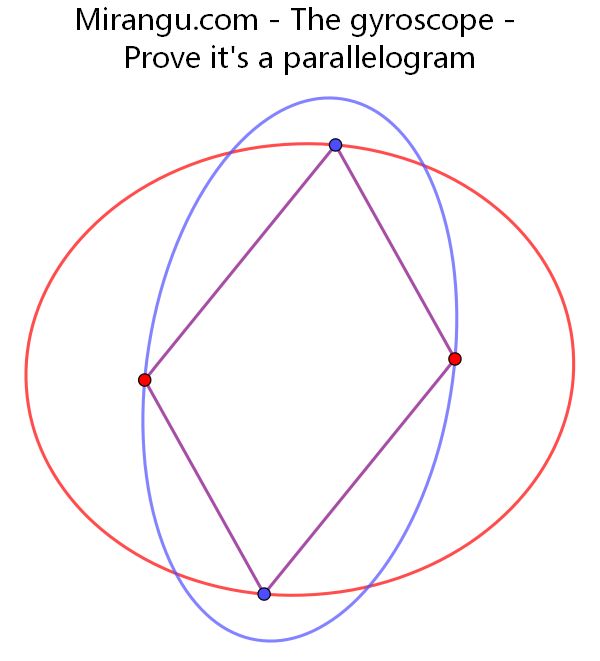
Two ellipses go through each others focal points. Prove that the focal points are the vertices of a parallelogram.
Categories
The Pappus eggs
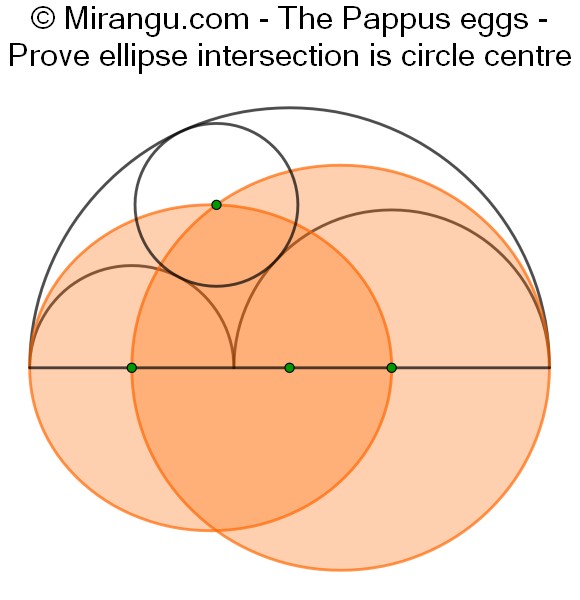
Three semicircles and a circle with their centres. Two orange ellipses with focal points in the semicircle centres (they share the middle one). Prove that their upper intersection point coincides with the circle centre.
Categories
The sliding ladder
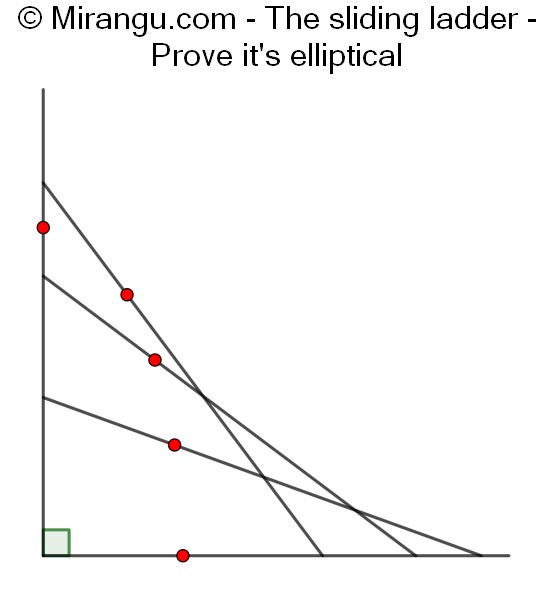
A ladder seen from the side is sliding down a wall. Prove that a fixed point on the ladder traces part of an ellipse.