Start with an acute triangle and form a new triangle from the points of tangency of its inscribed circle. Continue this process to make make the triangle with blue vertices. What is the maximum possible angle at a blue vertex?
Falling in
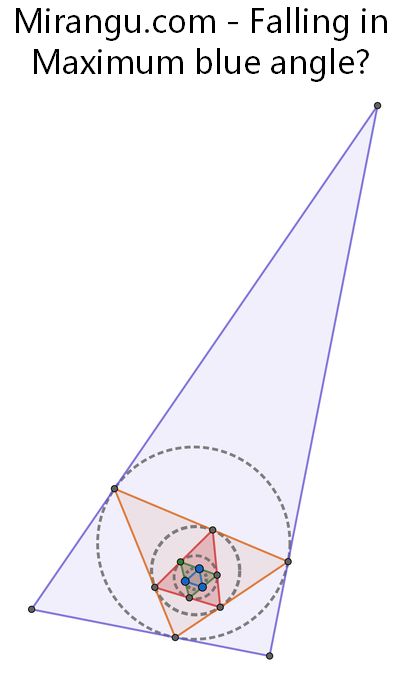

Start with an acute triangle and form a new triangle from the points of tangency of its inscribed circle. Continue this process to make make the triangle with blue vertices. What is the maximum possible angle at a blue vertex?
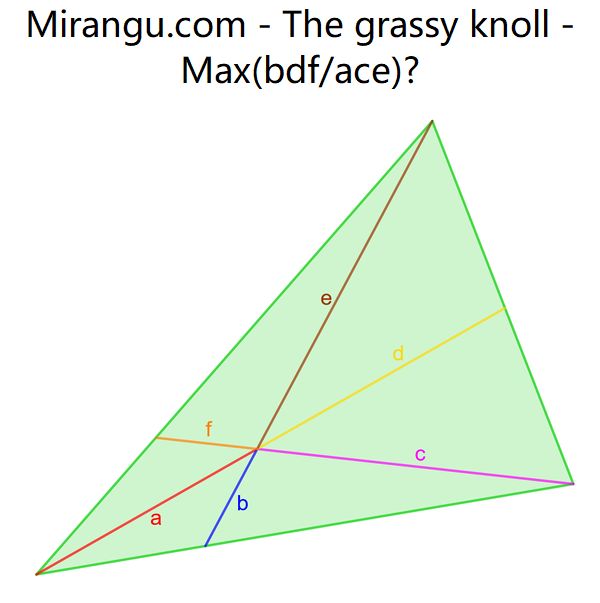
A triangle with three cevians that are concurrent in an arbitrary interior point. What is the maximum value of bdf/ace?
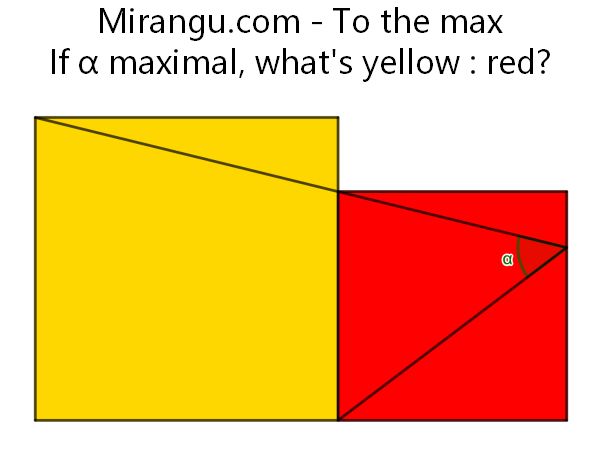
Two squares and two line segments. If the angle α is maximal, what is yellow : red?
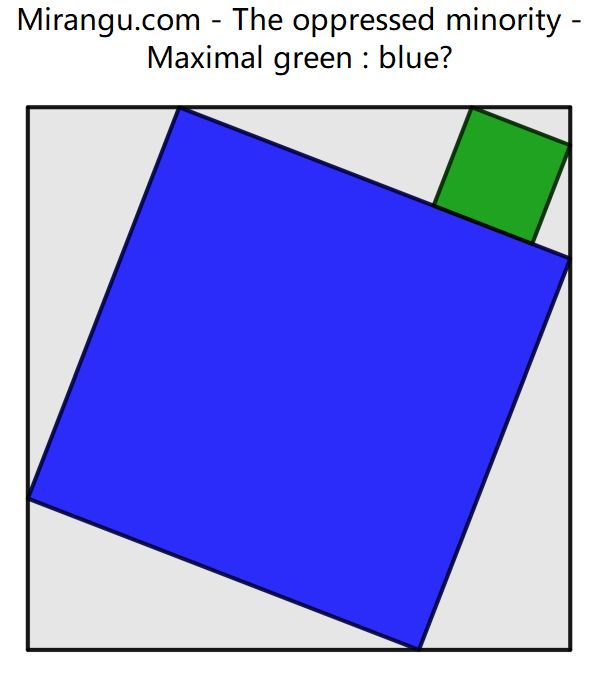
A square with two inscribed squares. What is the maximal proportion green : blue?
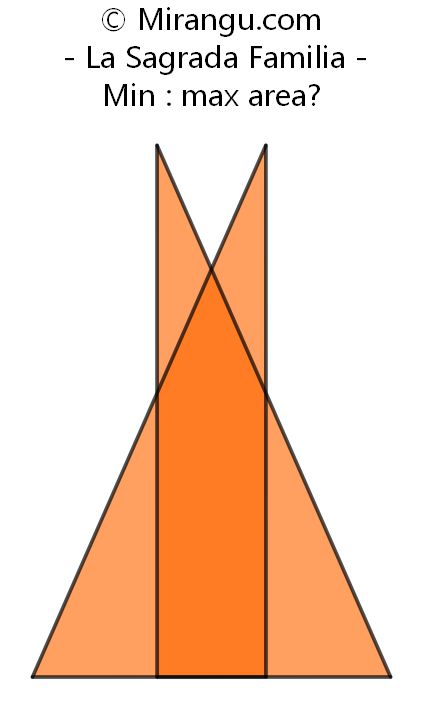
Two congruent right triangles on a common baseline have an overlap of variable size. What is the proportion of the minimal area to the maximal area?

A square containing a red square of variable size sharing a vertex with a blue rectangle. What is the maximal blue fraction?
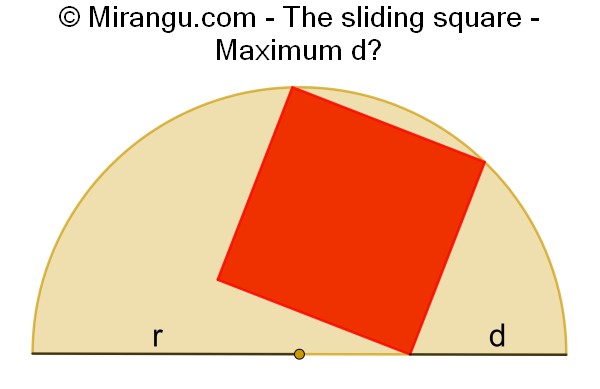
A square of variable size inscribed in a semicircle of radius r. What is the maximum distance d of the lowest square vertex to the nearest semicircle corner?
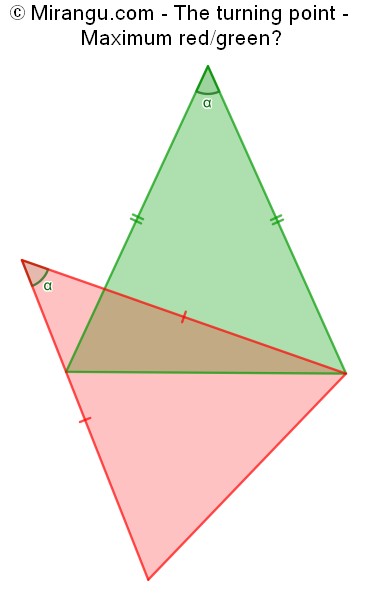
Two isosceles triangles share a vertex. What is the maximum of their area proportion red/green?
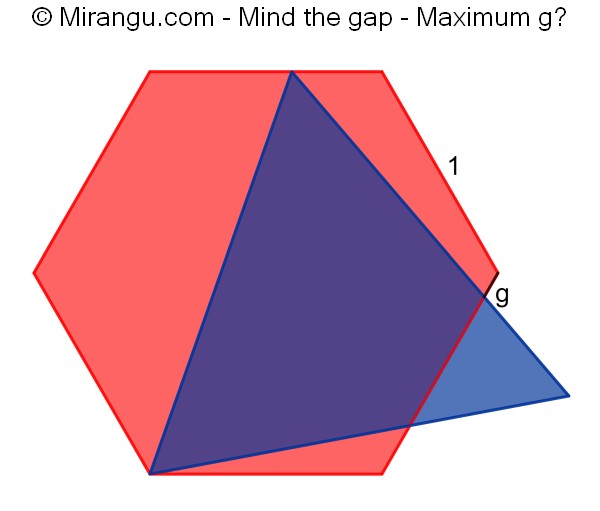
A regular hexagon with an equilateral triangle sharing a vertex and having a vertex somewhere along the opposite side. What is the maximum length of line segment g?
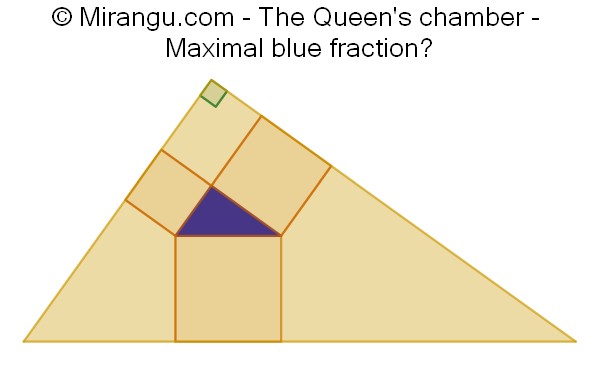
A right triangle with three squares forming a smaller inner triangle. What is the maximal blue fraction?