An arbitrary point on the parabola y=x2. Shown are the tangent in that point and a line segment perpendicular to it. What is the minimal height h?
The Moroni minimum
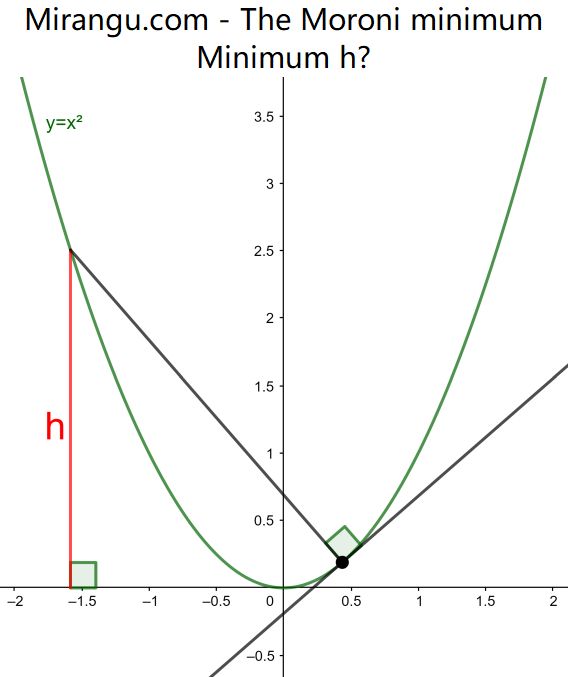

An arbitrary point on the parabola y=x2. Shown are the tangent in that point and a line segment perpendicular to it. What is the minimal height h?
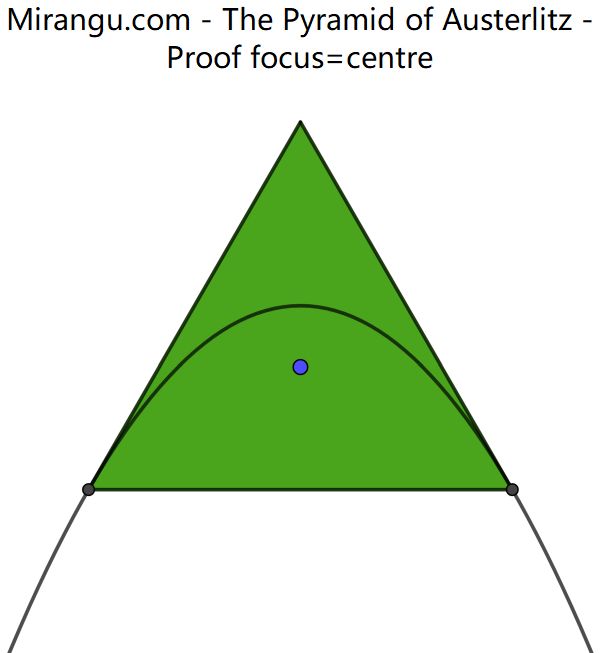
An equilateral triangle and a parabola that is tangent to two of its sides in two vertices. Proof that the triangle centre coincides with the parabola focus.
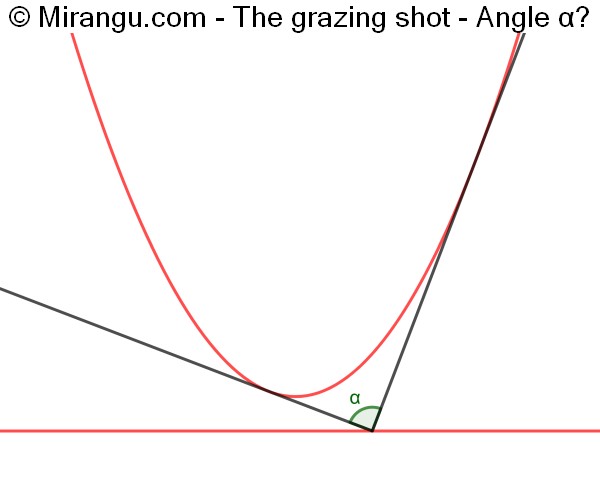
A parabola and its directrix in red. Two tangents intersect at a point on the directrix. What’s the angle α?
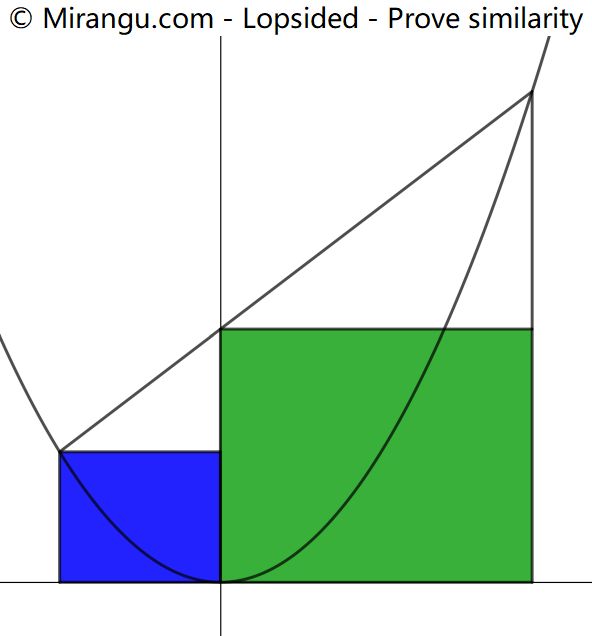
The apex of a parabola is the shared vertex of two rectangles. Proof that the rectangles are similar.
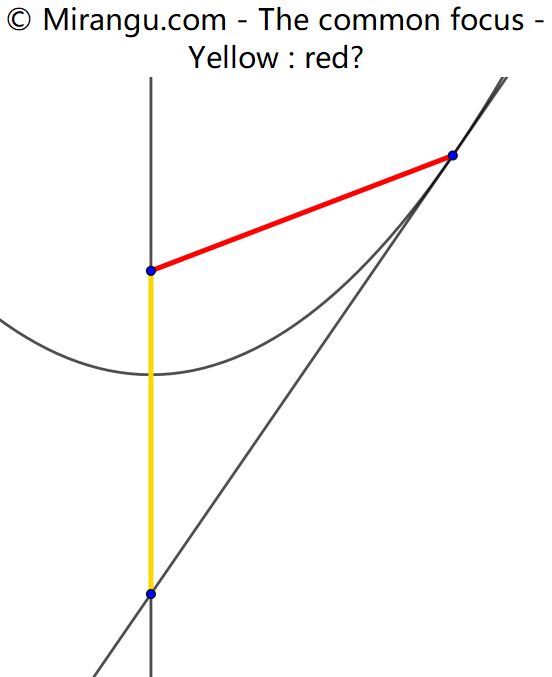
A parabola, its symmetry axis and a tangent. Yellow connects the focus to the intersection point. Red connects the focus to the tangency point. What’s yellow : red?
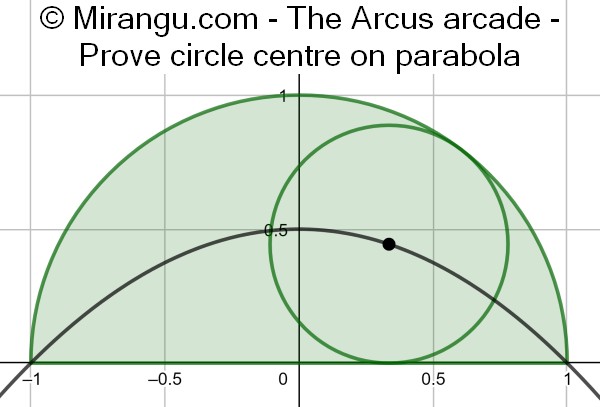
A semicircle and an inscribed circle. Prove that the circle centre is on the parabola.
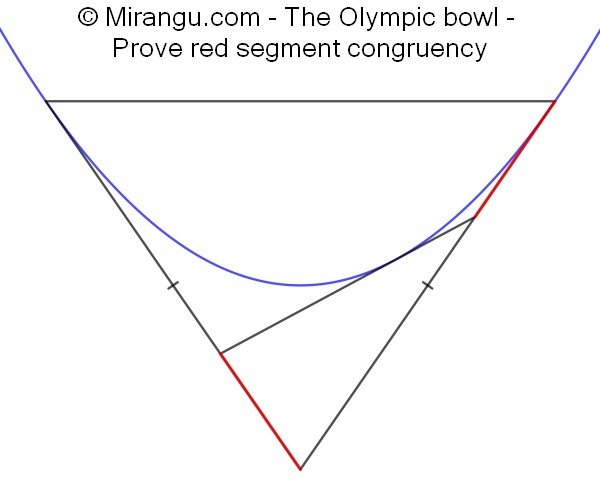
A parabola is tangent to the equal sides of an isosceles triangle in its equal vertices. Another tangent is drawn as shown. Prove that the red line segments are congruent.
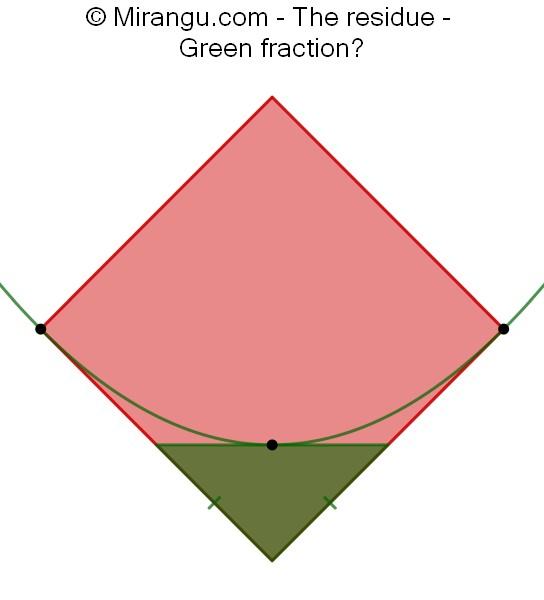
A parabola is tangent to two sides of a square and to the hypotenuse of an isosceles triangle. The three tangency points are shown. What fraction of the square is green?

A parabola passing through a square’s bottom vertices and tangent to its top side. What fraction is blue?
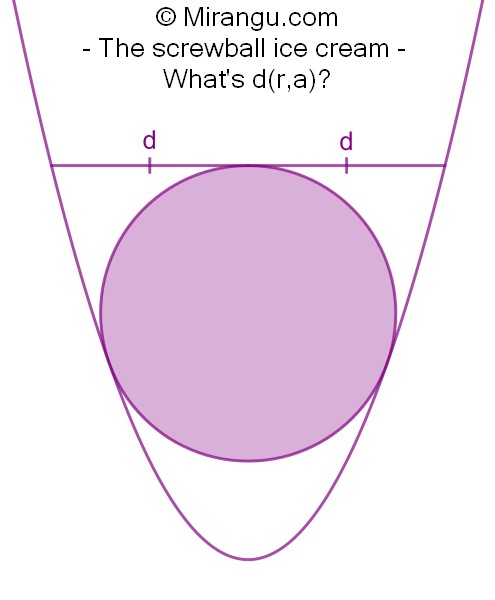
A circle of radius r touching both sides of a parabola having focal length a. A line segment tangent to the circle is split in two equal segments of length d. What is d in terms of r and a?