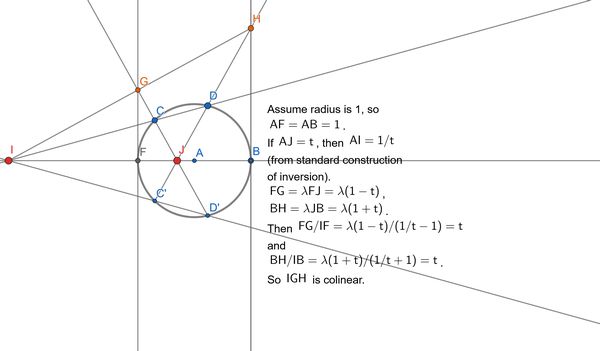
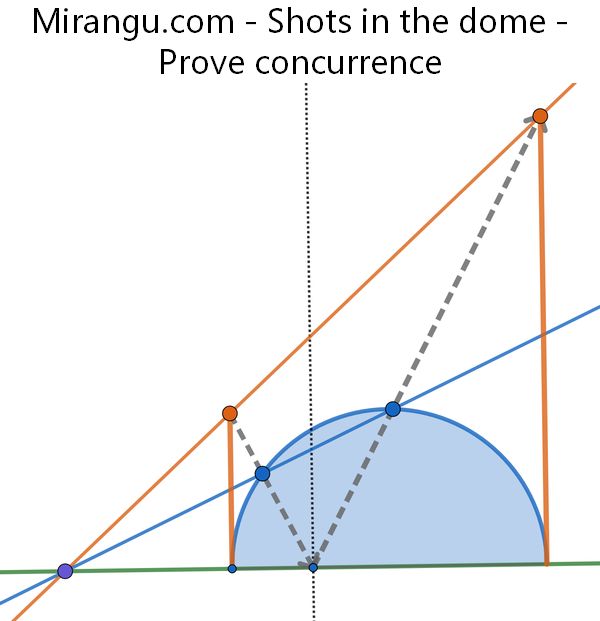
A beam from the top of one tower cuts through the dome, reflects off the ground, and hits the top of the other tower. Show that the line connecting the orange dots, the line connecting the blue dots, and the ground line are concurrent.
Scroll down for a solution to this problem.
Solution
Poem
Shots in the dome
Not enough weapons
To defend all this lifes
Only destruction
Of a country
And its cities
Because of our cowardice
Because of our egoism
Because of our fears
The dome is pierced
The dome is dying
One reply on “Shots in the dome”
There is even an “easier” solution that applies a projective transformation, respecting the circle, but moving the reflection point on the ground to the middle of the dome. Then the orange, blue, and green lines will obviously be parallel, because the diagram will be symmetric about the vertical diameter, so projectively concurrent, and the actual blue, green, and orange lines must go through a common finite point.