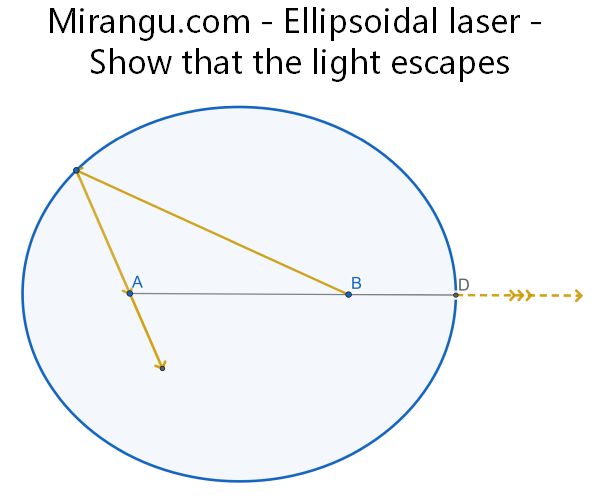
The inside surface of an ellipse is a perfect mirror. There is a pin-hole at an end of the diameter. Show that a light ray emitted from either focus will exit the enclosure via the pin-hole, perhaps after bouncing through the foci several times.
Click for Extra Credit Problems.
Scroll down for a solution to this problem.
Solution
Consider the continuous function g from the ellipse to itself defined by following a ray from a given point x through A, reflecting at the ellipse back through B and on to the next point, g (x), on the ellipse. The function has two fixed points, D1 and E1, the end points of the diameter. Otherwise, g (x) will be strictly between x and E1. Each sequence x, g (x), g (g (x)), … will be strictly decreasing (towards E1) and have a limit x′, which because of the continuity of g will be a fixed point of g , and thus the limit x′ must be E1 itself. No matter how small the pin hole is, eventually the iterates must get close enough to E1 to pass through the pin hole.