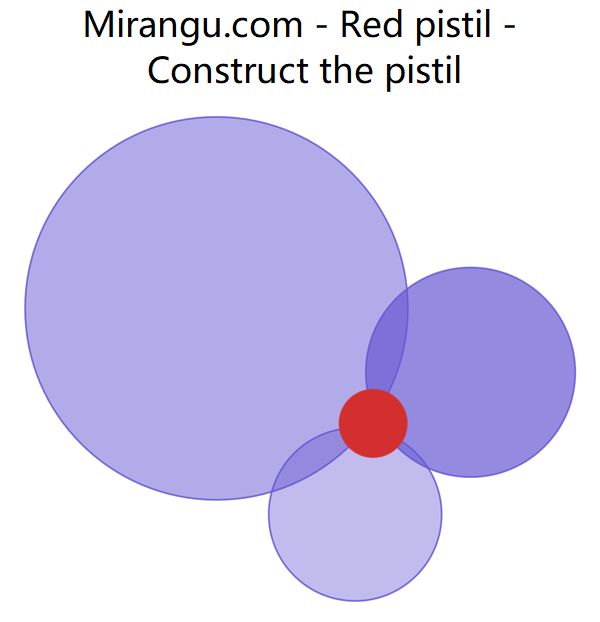
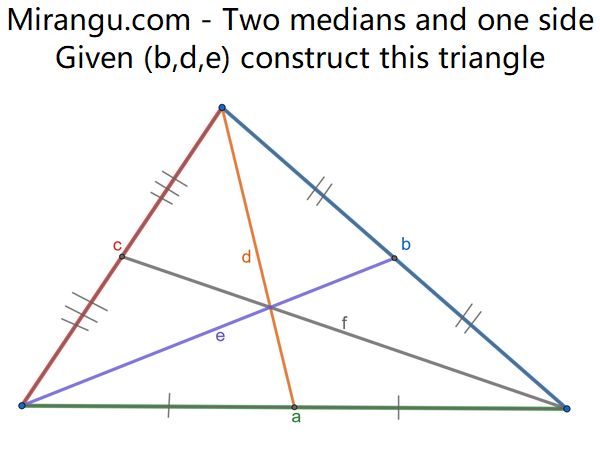
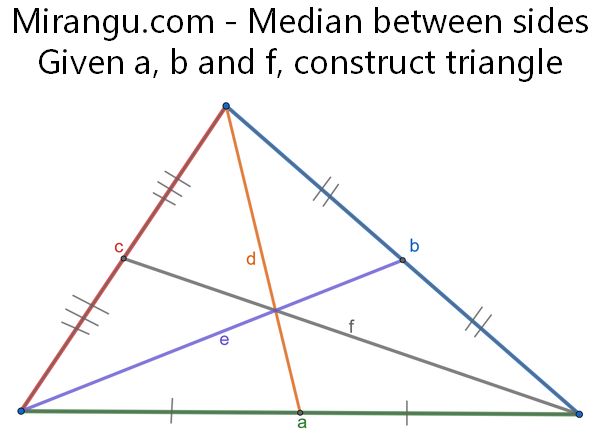
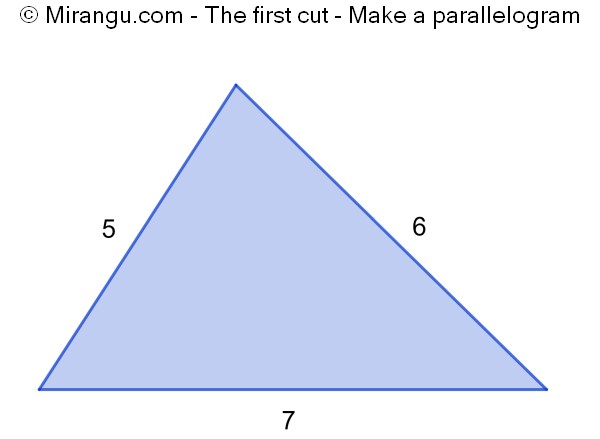
Three circular petals surround a red pistil which is orthogonal to each of the petals. Given the petals, construct the pistil. (You may assume that you are given a direct way to construct a tangent line from an exterior point to any circle.)
Given the blue square AEFI and a point B inside, show that the intersection H of the red and purple semicircles will be a corner of a square containing B on one side and A on another, and sharing the corner I with the blue square.
Given a point A on a circle and another point I in the interior of the circle, find two other points B, C on the circle so that I is the incentre of the triangle ABC. Find B and C as the intersection points between the given circle and some other circle.
Given green and blue discs, construct a red region so that for every ray leaving L stays in the blue region exactly as long as it does in the pink region. (Namely, KM = OL.)
A triangle has sides a,b,c and the medians d,e,f ending at those sides, respectively. Given only the lengths (b,d,e) construct the triangle (a,b,c). (Start with a triangle with side lengths determined in some manor from the given 3 lengths.)
A triangle has sides a,b,c and the medians d,e,f ending at those sides, respectively. Given the lengths (a,b,f) construct the triangle. (Start with a triangle with side lengths determined in some manor from the given 3 lengths.)
Using one straight cut, divide this triangle in two pieces. Paste them together to form a parallelogram with perimeter 19.