Two regular pentagons share a vertex. What’s the angle α?
Tipping point II
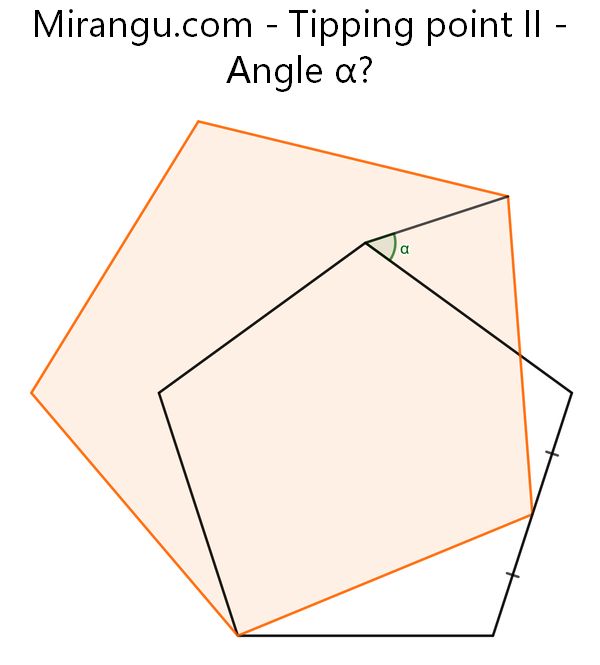

Two regular pentagons share a vertex. What’s the angle α?
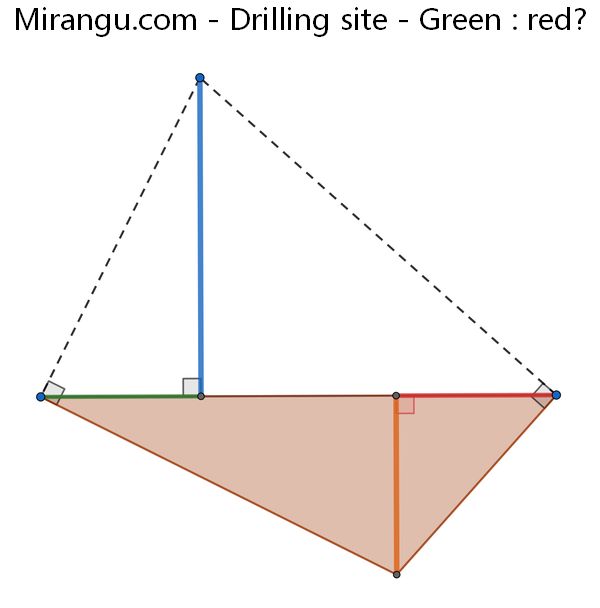
A blue flagpole is erected near a drilling site. Lines are drilled perpendicular to the flagpole guy wires and meet at the bottom of the orange drilling pipe. What is the ratio of distances green to red?
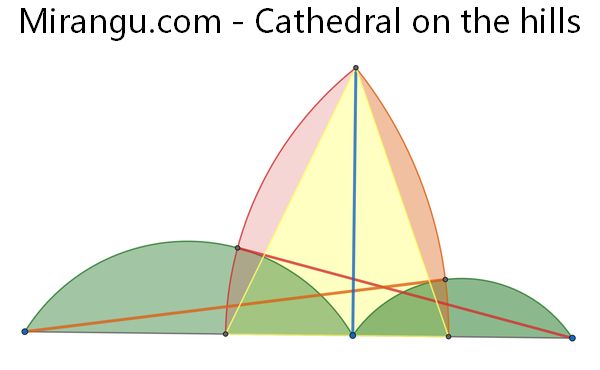
A cathedral is erected on two hills, the side circular arcs whose centers are the hill ends, and so that the right (and left) side arcs are orthogonal. Show that the tip of the spire is directly above where the hills meet.
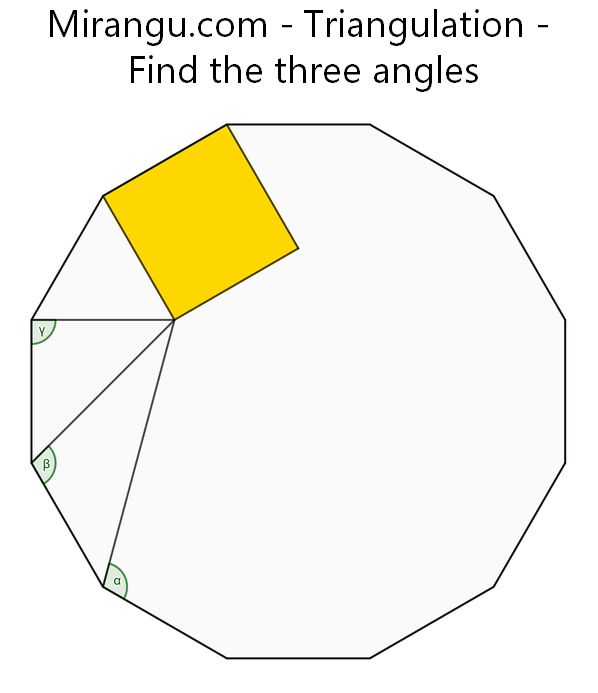
A regular dodecagon contains a yellow square. Find the three angles α, β and γ.
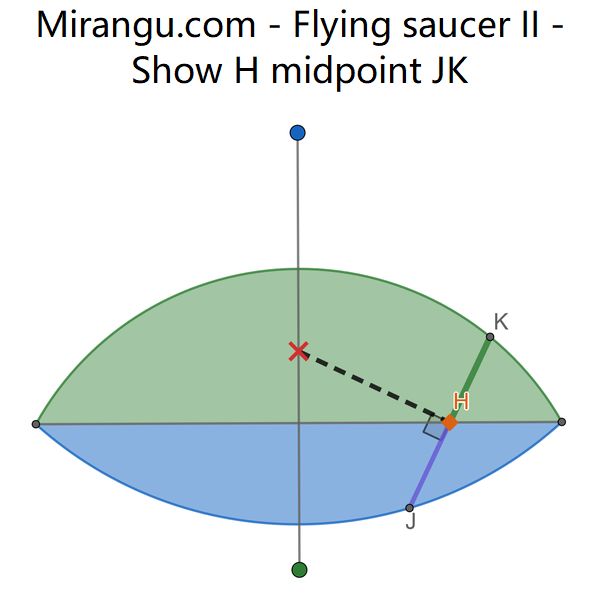
If X is the midpoint of the segment connecting the centers of the upper and lower arcs, and JK is perpendicular to XH, then show that H is the midpoint of JK.
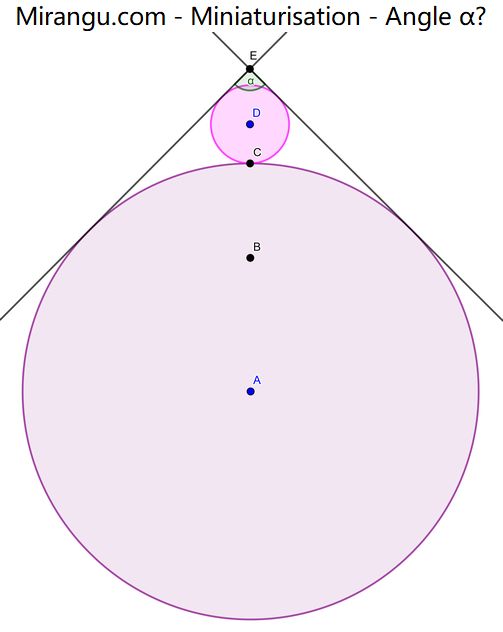
Two tangent circles and two common tangents. A and D are centres. B is midpoint of AD. C is midpoint of BE. What is the angle α?
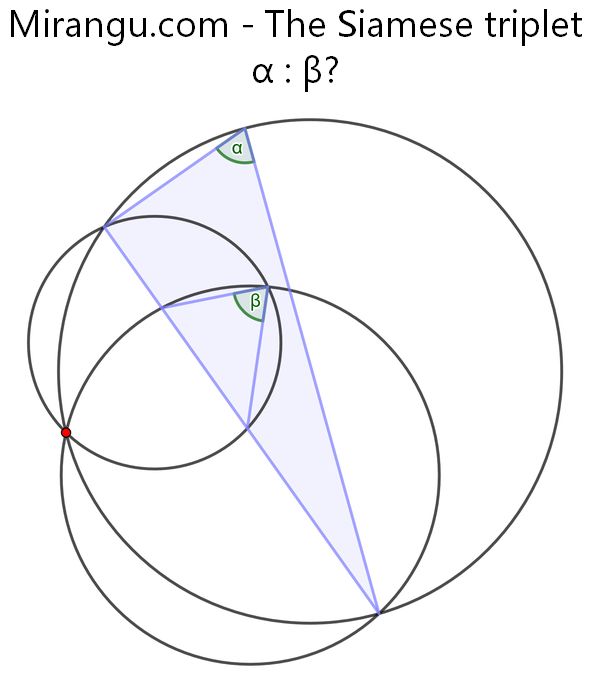
Three circles with a common intersection point and two triangles. What is α : β?
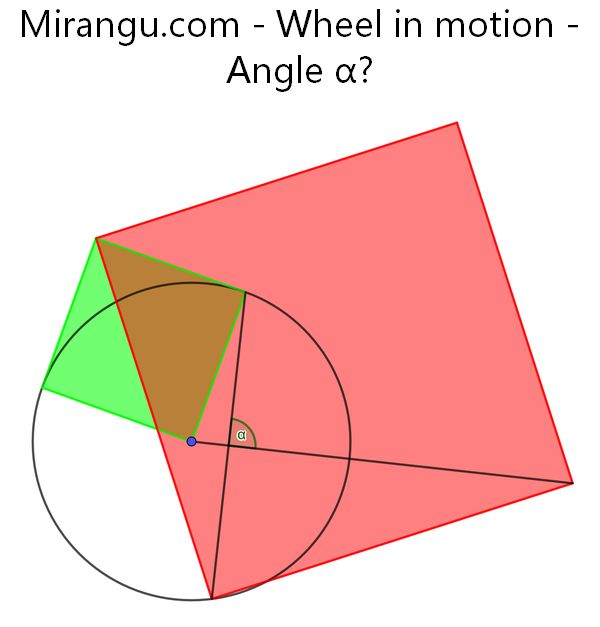
A circle with its centre and two squares sharing a vertex. What’s the angle α?
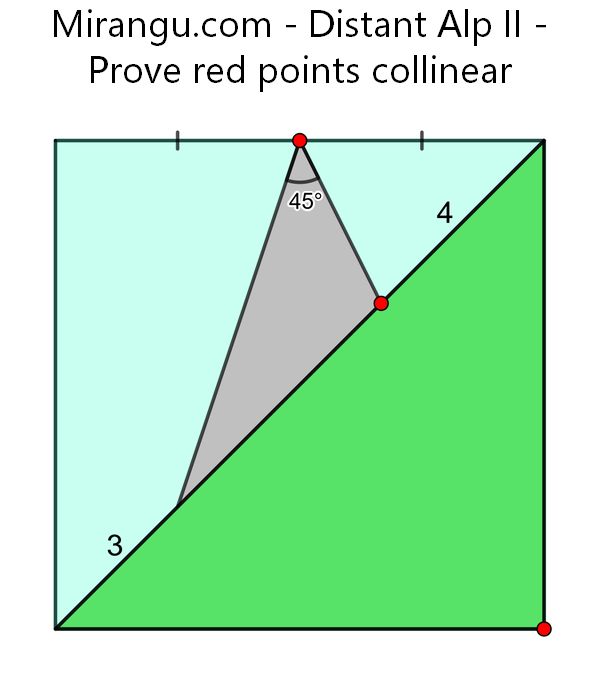
A square with its diagonal. Prove that the three red points are collinear.
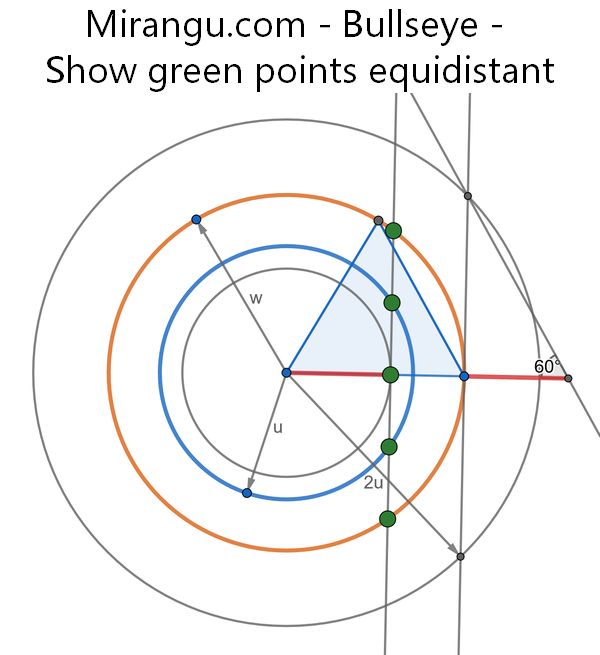
Blue and orange concentric circles intersect a vertical line in green dots. Show that the dots are equally spaced, given that the red intervals shown are of equal length. (The largest circle has radius 2u.)