The odd regular polygons are stacked together, in increasing order, zigzagging to form a telescope that extends forever! What is the limiting angle (with respect to the horizontal) at which the telescope points?
The telescope
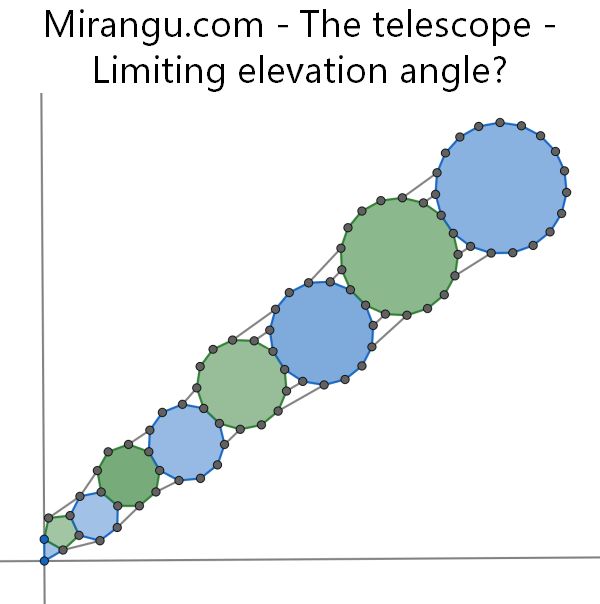

The odd regular polygons are stacked together, in increasing order, zigzagging to form a telescope that extends forever! What is the limiting angle (with respect to the horizontal) at which the telescope points?
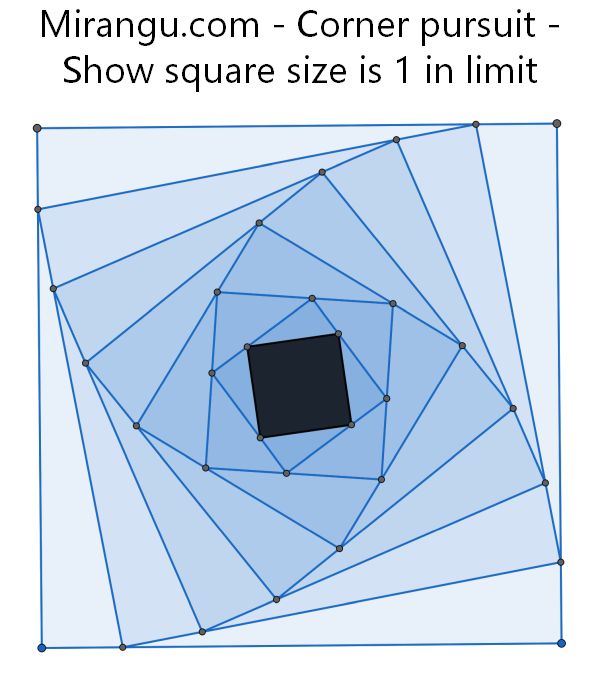
Four corners of a square pursue each other clockwise, and after each unit step mark out the new smaller square. Show that the squares sizes in the sequence decrease in size to 1 in the limit.
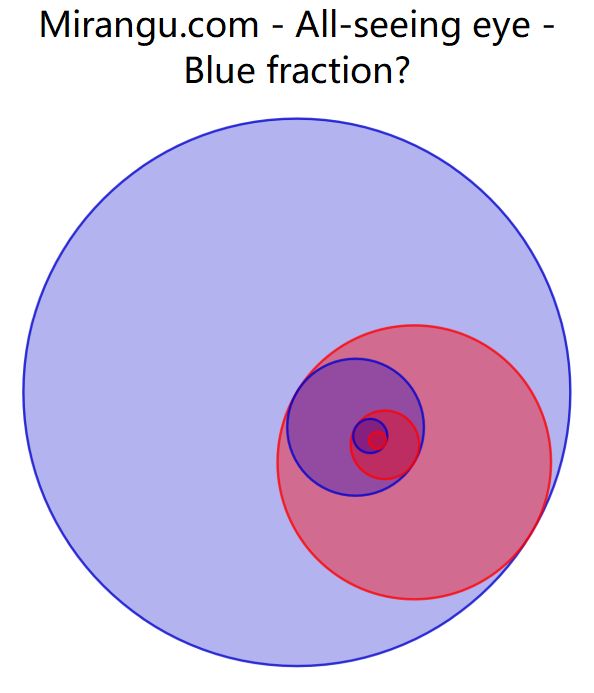
If the radius shrinks by the factor 1/2 for each smaller circle, what fraction of the whole area is represented by all the blue crescents (separated by the red crescents)? Assume the circles keep going inward forever.
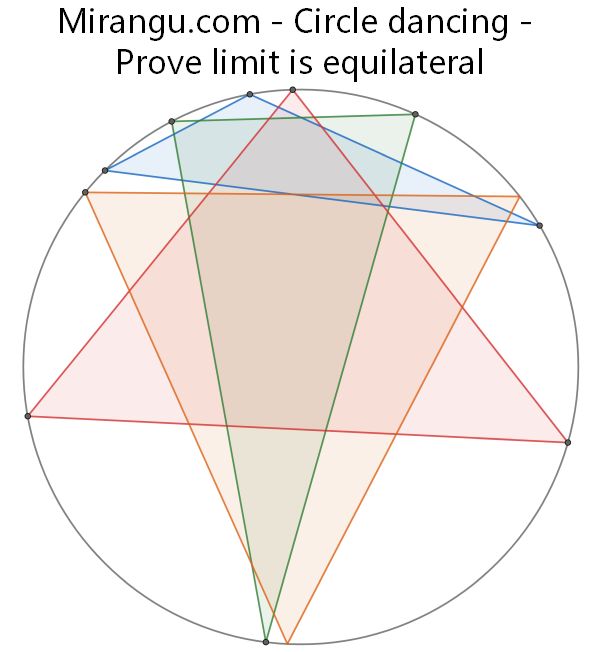
Start with a blue triangle, and form the green triangle whose vertices bisect each circular arc connecting blue vertices. Similarly, make the red triangle from the green, and the orange triangle from the red. Prove the triangle becomes equilateral in the limit.
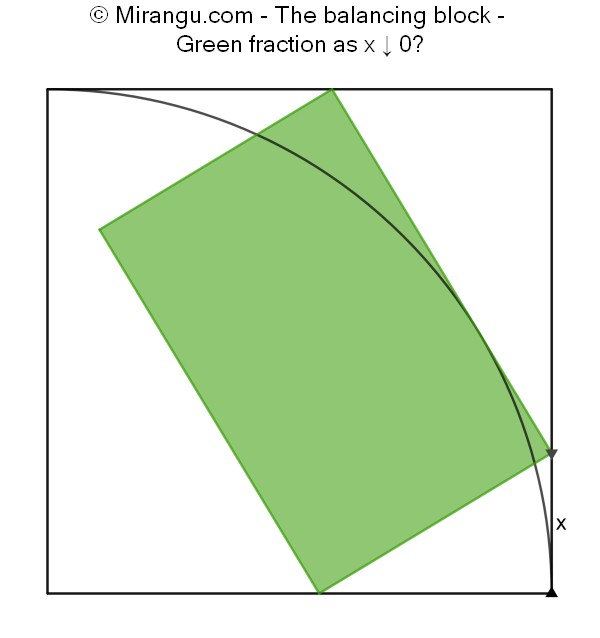
A rectangle inside a square. One of its sides is tangent to the quarter circle. What fraction is green as x approaches 0?
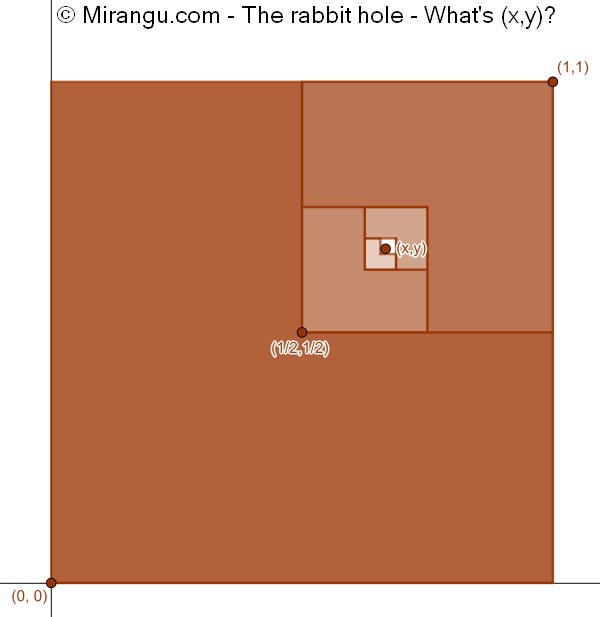
Three quarters of a unit square placed at the origin are shaded as shown. The remaining quarter is treated similarly but mirrored, and so on to infinity. What are the coordinates of the vanishing point?