Two squares sharing a vertex and two overlapping coloured quadrilaterals from square side midpoints. What is the area proportion of the blue and the red quadrilateral?
Quad stretches
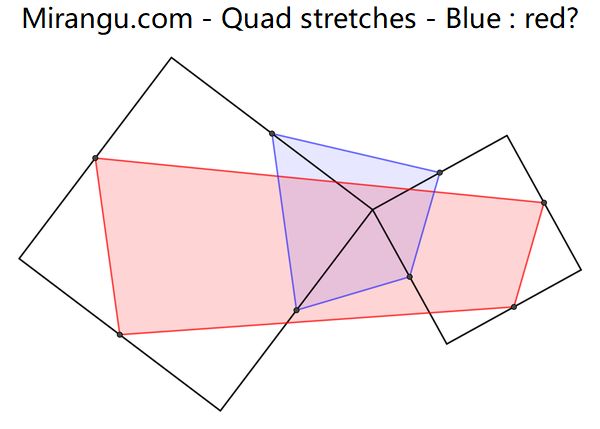

Two squares sharing a vertex and two overlapping coloured quadrilaterals from square side midpoints. What is the area proportion of the blue and the red quadrilateral?
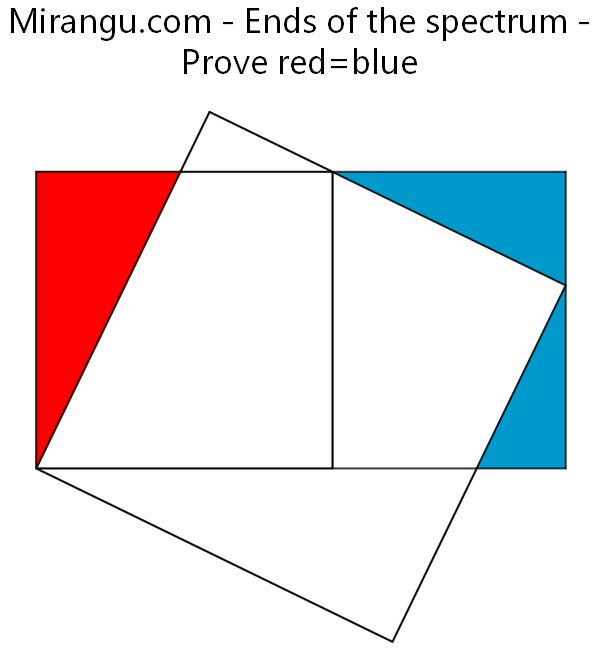
Two squares and a rectangle. Prove that red = blue.
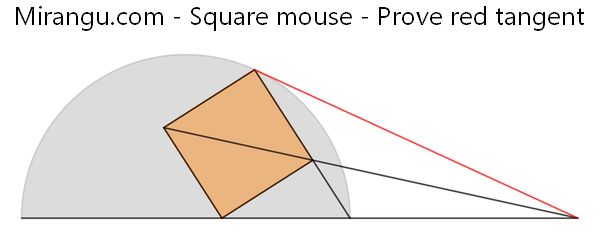
A semicircle and a square with extended side and diagonal. Prove that the red line segment is tangent to the semicircle.
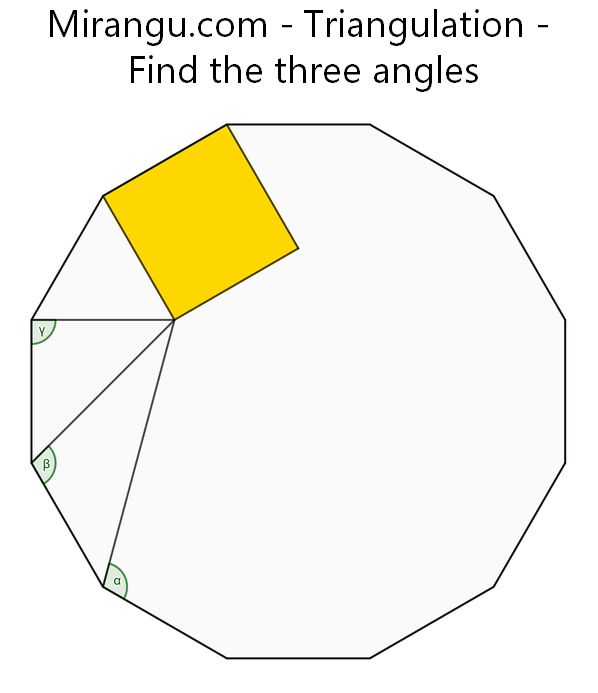
A regular dodecagon contains a yellow square. Find the three angles α, β and γ.
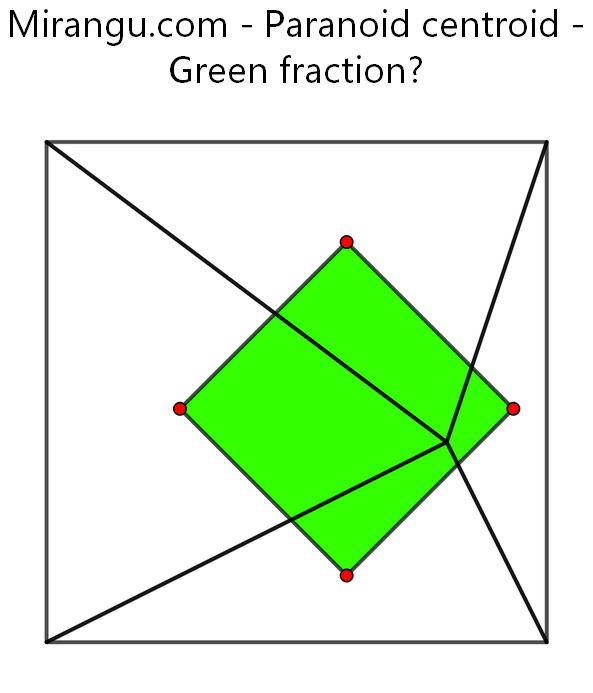
A square is divided in four triangles of which the red centroids are shown. What fraction is green?
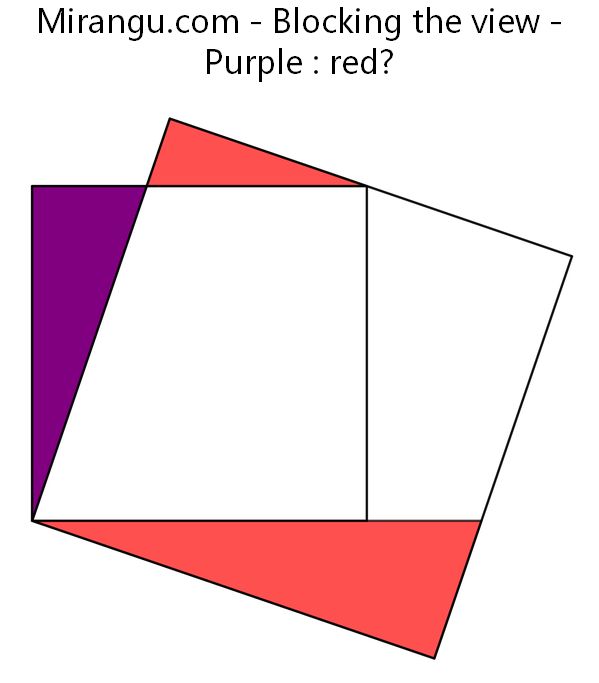
Two squares and one extended side. What is purple : red?
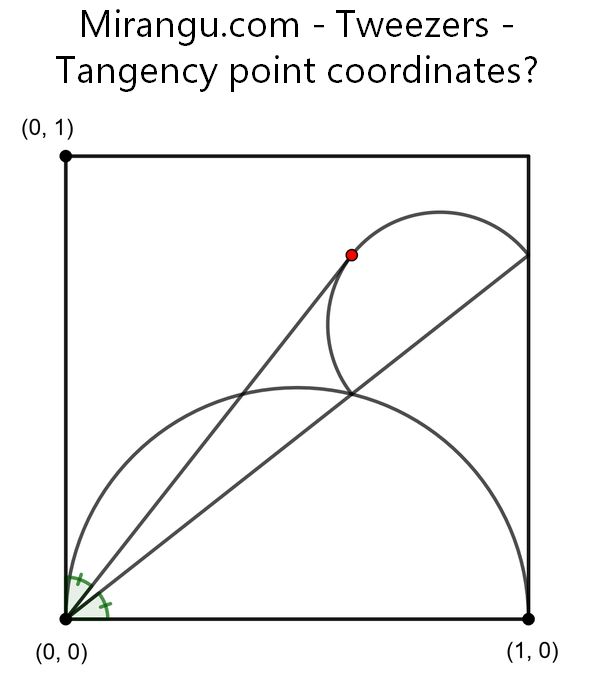
A square with two semicircles. The smaller one has an extended diameter and a tangent. What are the coordinates of the tangency point?
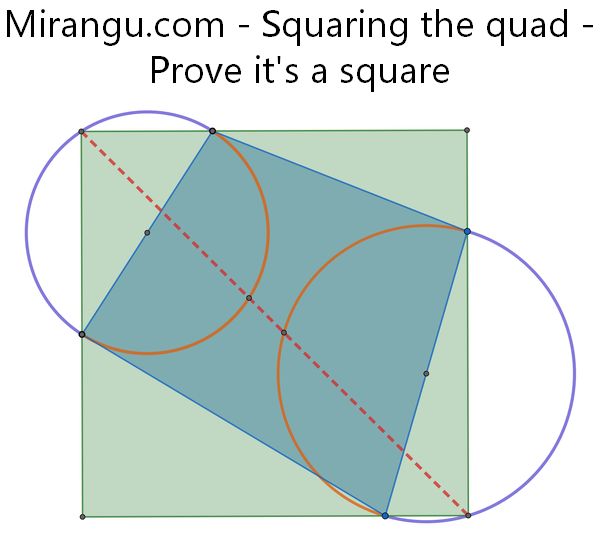
Form inward semicircles (orange) and outward semicircles (purple) on two opposite sides of a quadrilateral. Connect the midpoints of the orange arcs, intersecting with the purple arcs. Show that you obtain two corners of an enclosing square.
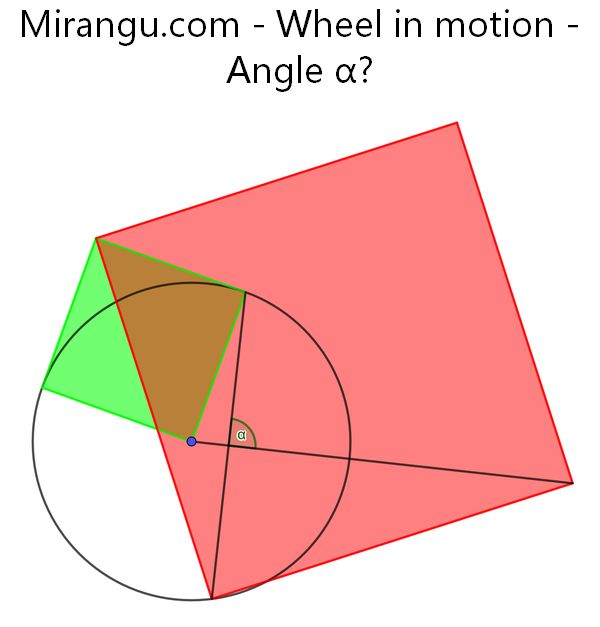
A circle with its centre and two squares sharing a vertex. What’s the angle α?
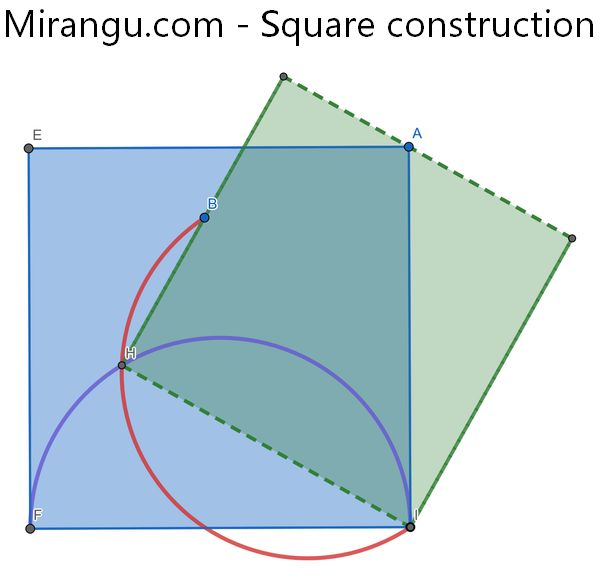
Given the blue square AEFI and a point B inside, show that the intersection H of the red and purple semicircles will be a corner of a square containing B on one side and A on another, and sharing the corner I with the blue square.