Two squares sharing a vertex and two overlapping coloured quadrilaterals from square side midpoints. What is the area proportion of the blue and the red quadrilateral?
Quad stretches
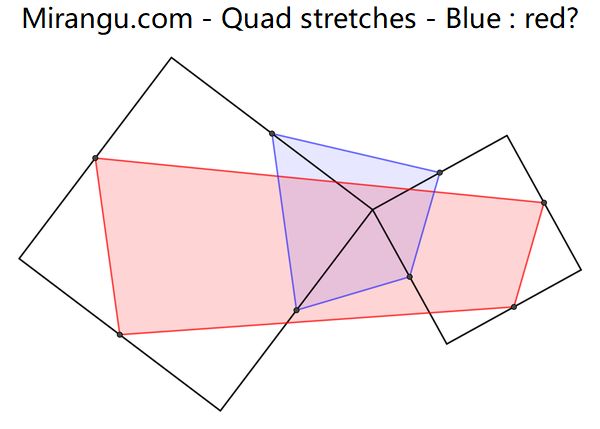

Two squares sharing a vertex and two overlapping coloured quadrilaterals from square side midpoints. What is the area proportion of the blue and the red quadrilateral?
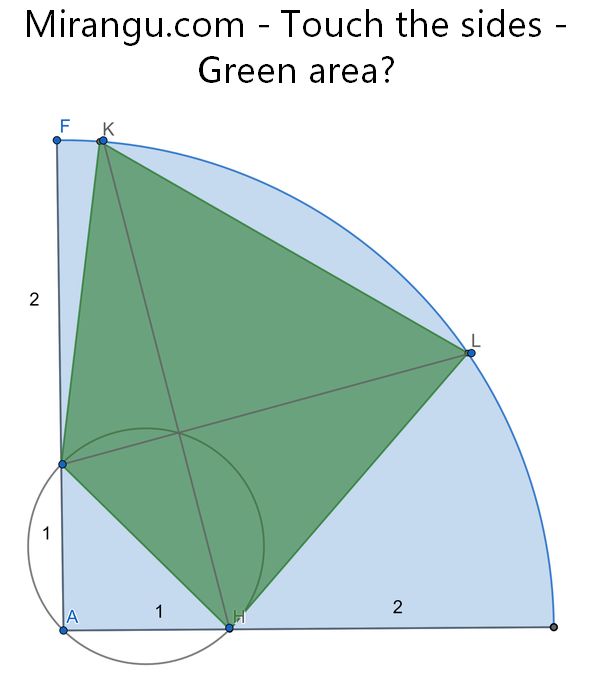
What is the area of a green quadrilateral that fits inside a quarter circle, and has perpendicular diagonals?
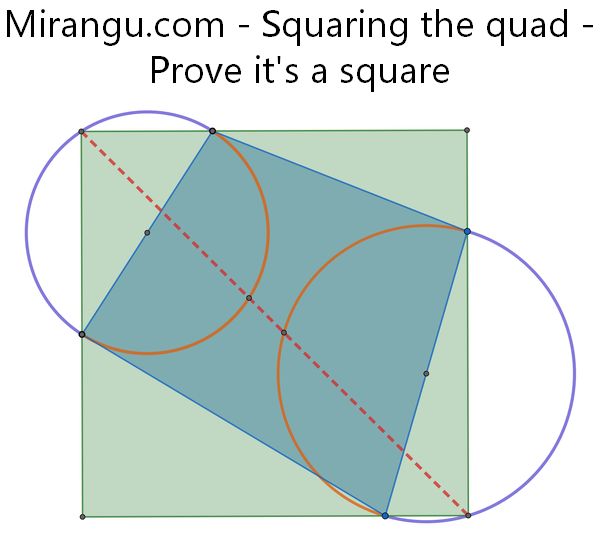
Form inward semicircles (orange) and outward semicircles (purple) on two opposite sides of a quadrilateral. Connect the midpoints of the orange arcs, intersecting with the purple arcs. Show that you obtain two corners of an enclosing square.
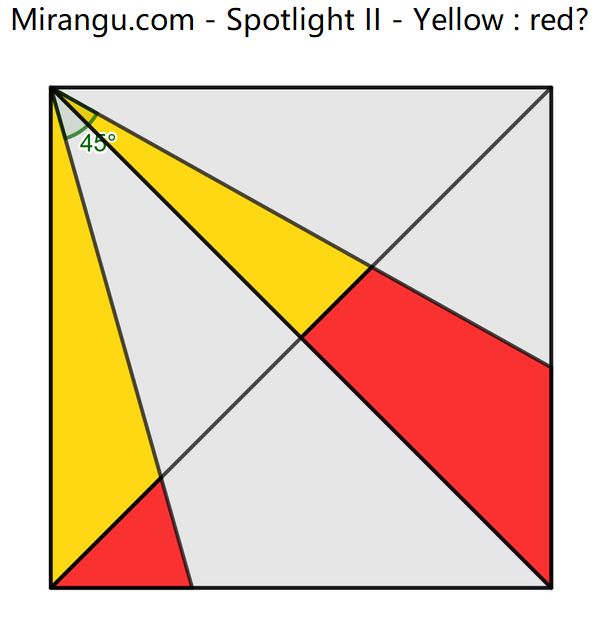
A square is divided in several triangles and quadrilaterals. What is yellow : red?
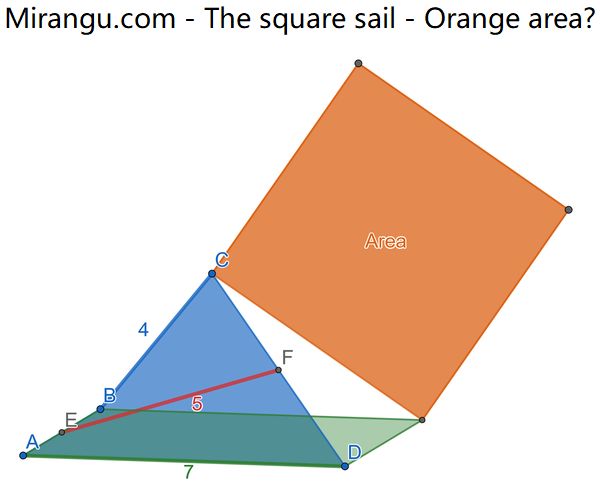
A quadrilateral and a parallelogram share two sides, and a vertex from each determine the orange square. The lengths BC, EF, AD are 4,5,7 respectively, where E and F are midpoints of AB and DC. What is the orange area?
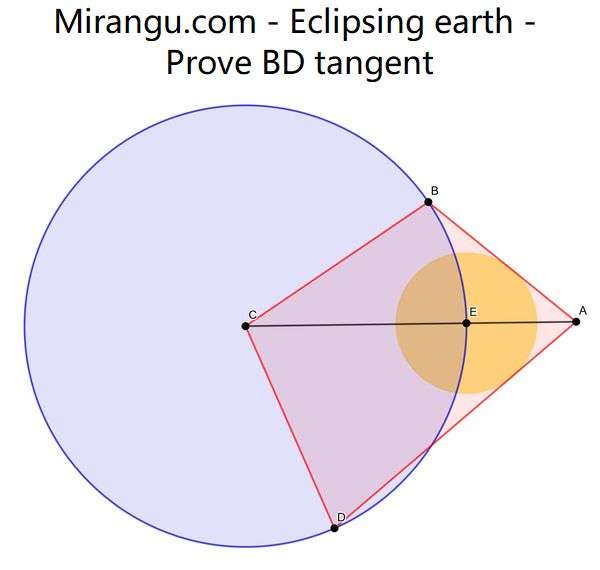
Two circles with their centres. The quadrilateral ABCD is cyclic and has two sides tangent to the small circle. Prove that BD is also tangent.
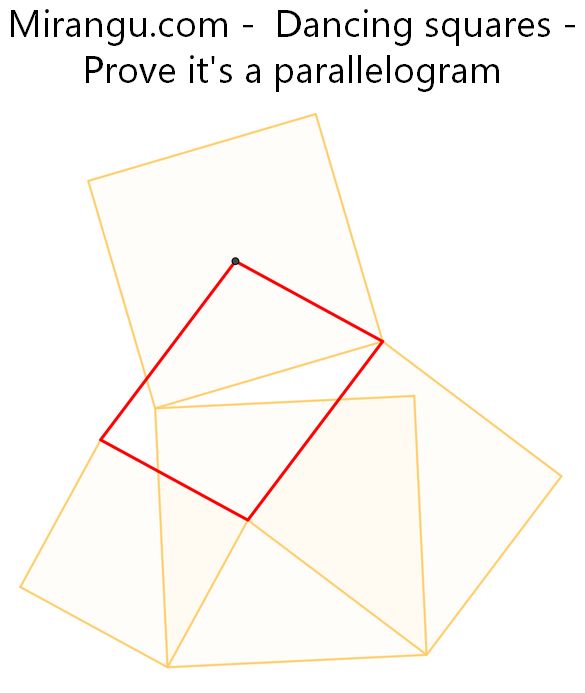
Four squares and one centre. Prove that the red quadrilateral is a parallelogram.
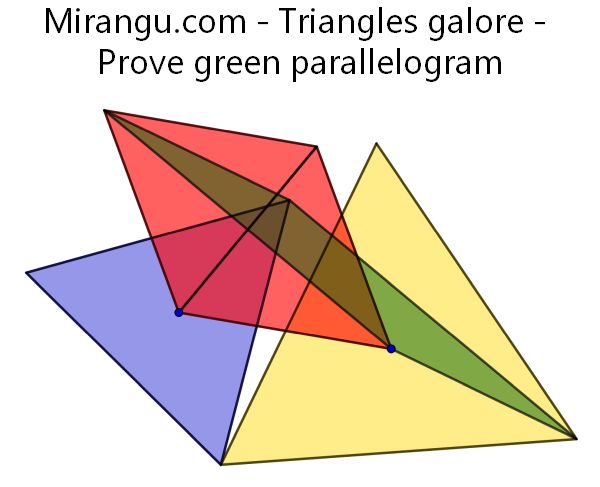
Four equilateral triangles. Two centres are shown. Prove that the green quadrilateral is a parallelogram.
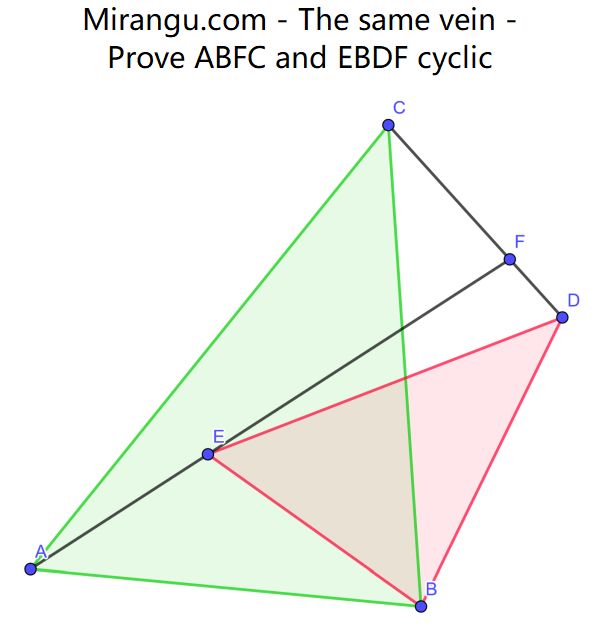
Two similar triangles ABC and EBD. Two line segments meet at point F. Prove that ABFC and EBDF are cyclic quadrilaterals.
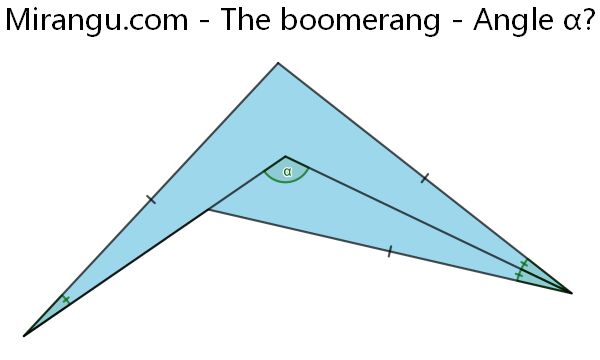
A quadrilateral and a triangle. What’s the angle α?