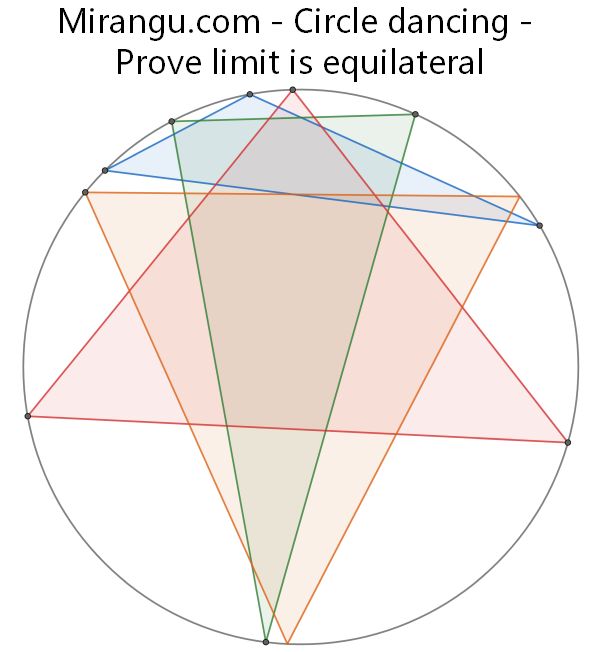
Start with a blue triangle, and form the green triangle whose vertices bisect each circular arc connecting blue vertices. Similarly, make the red triangle from the green, and the orange triangle from the red. Prove the triangle becomes equilateral in the limit.
Scroll down for a solution to this problem.
Solution
Name the angles in the triangle a, b and c. Then the first iteration is stepping to (b+c)/2, (c+a)/2 and (a+b)/2. But b+c = 180-a. So iteration is really just x -> 90 -(x/2). Or equivalently 60-x -> (60-x)/2. So every angle converges to 60.
One reply on “Circle dancing”
This problem is a follow-up to the earlier problem:
https://mirangu.com/star-from-the-collision-of-spherical-nebulae/#more-8288
where the triangle ABC produces a second triangle DEF,
and the rule for the iteration is the same as here.