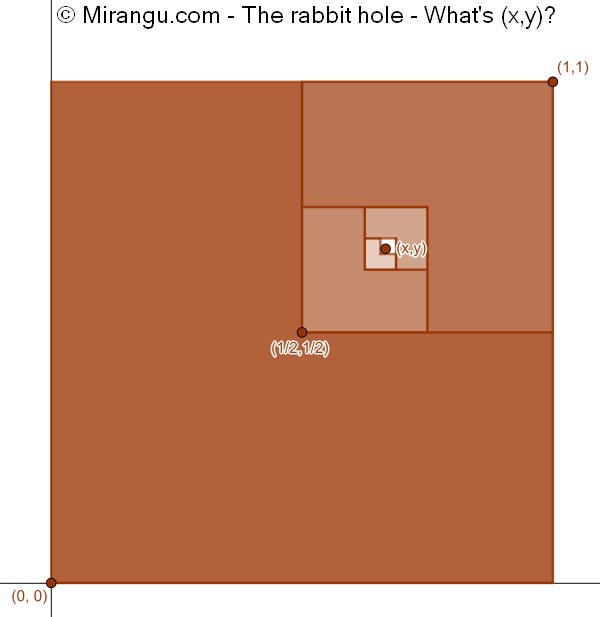
Three quarters of a unit square placed at the origin are shaded as shown. The remaining quarter is treated similarly but mirrored, and so on to infinity. What are the coordinates of the vanishing point?
Scroll down for a solution to this problem.
Solution
The vanishing point is at (2/3,2/3).
From reflection symmetry in the diagonal, it is clear that x=y. Now if you look at the top vertex of the three-quarter shape, its x-coordinate goes from 0 to 1 to 1/2 to 3/4 to 5/8 and so on as the shape gets smaller. This has the pattern 1-1/2+1/4-1/8+…. In other words it is the sum of (-1/2)n with n=0,1,… This is called the Geometric series and it tends to 1/(1+1/2)=2/3 as n goes to infinity.
Poem
The rabbit in it’s hole
With it’s ears so tall
And his eyes so small
The rabbit is jumping
With it’s twinkly nose
Here and there a jump he goes
Run run to that hole
Leading to Alice’s wonderland
And no one to understand
In deep soft sand
With tunnels dipped so deep
No end !