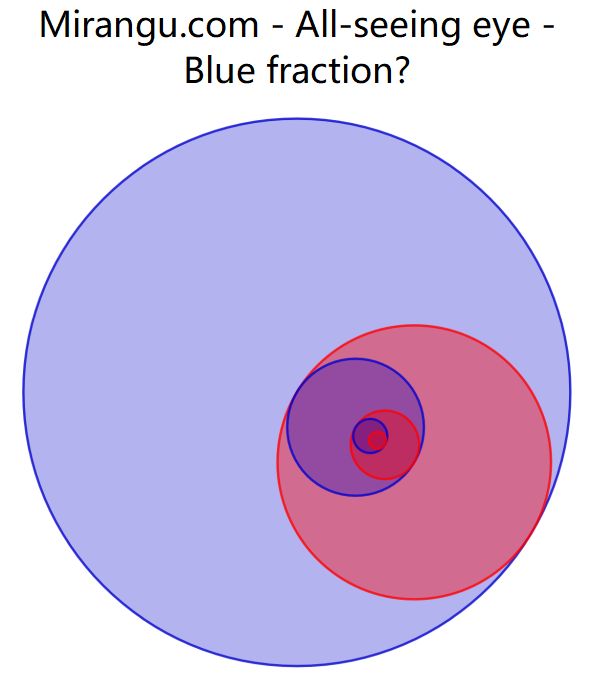
If the radius shrinks by the factor 1/2 for each smaller circle, what fraction of the whole area is represented by all the blue crescents (separated by the red crescents)? Assume the circles keep going inward forever.
Scroll down for a solution to this problem.
Solution
The blue fraction is 4/5.
Solution by Jason Elliot Benda
The area is proportional to the square of the linear measure, so it is (1/2)(1/2) each time, or 1/4. 1 – 1/4 + 1/16 … this is an infinite geometric series with first term 1 and common ratio –1/4, so the sum is (1) / (1 – (–1/4)) = 1 / (5/4) = 4/5.