The triangle ABC has orthocentre H, so that HA is an antenna above the green hill. The rectangle BCDE is inscribed in the circumcircle (ABC). Show that HA = CD = BE.
Antennas above and below
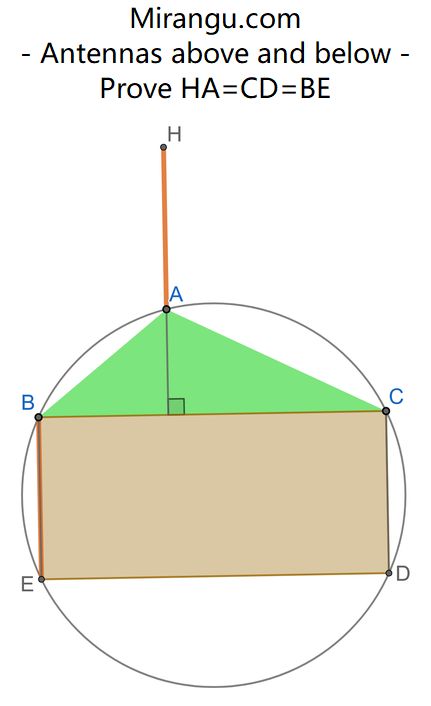

The triangle ABC has orthocentre H, so that HA is an antenna above the green hill. The rectangle BCDE is inscribed in the circumcircle (ABC). Show that HA = CD = BE.
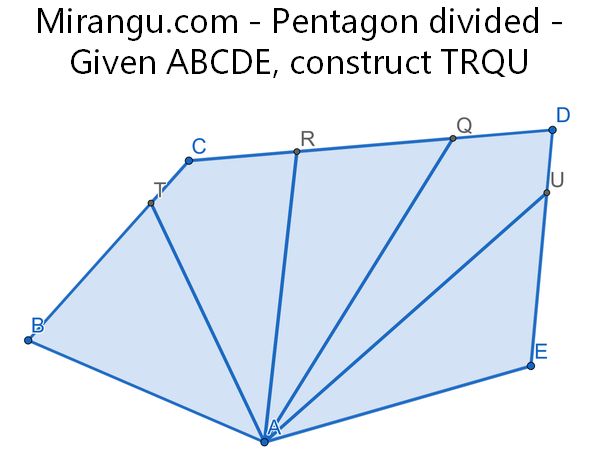
Given a pentagon ABCDE, construct the points T,R,Q,U such that the segments AT, AR, AQ, and AU divide the pentagon into five equal area pieces. (Using straight edge and compass. But you may divide a segment into a number of equal segments for free.)
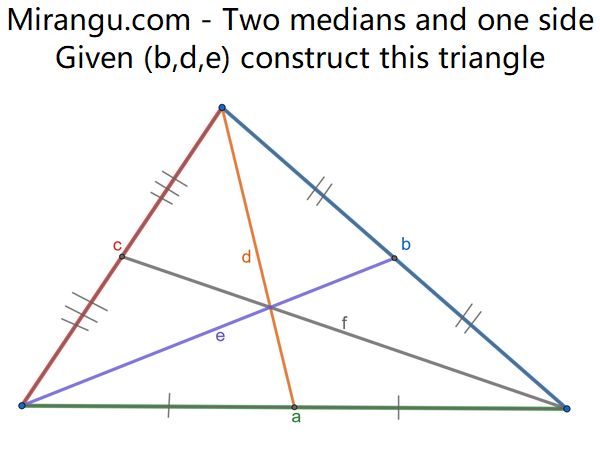
A triangle has sides a,b,c and the medians d,e,f ending at those sides, respectively. Given only the lengths (b,d,e) construct the triangle (a,b,c). (Start with a triangle with side lengths determined in some manor from the given 3 lengths.)
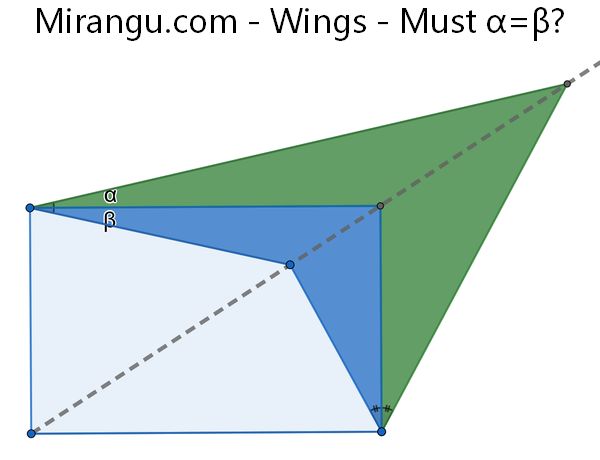
Two wings are attached to the corner of a rectangle, and have corners lined up with the diagonal of the rectangle. The angles at the lower wing tips are equal. Must α = β at the left wing tips?
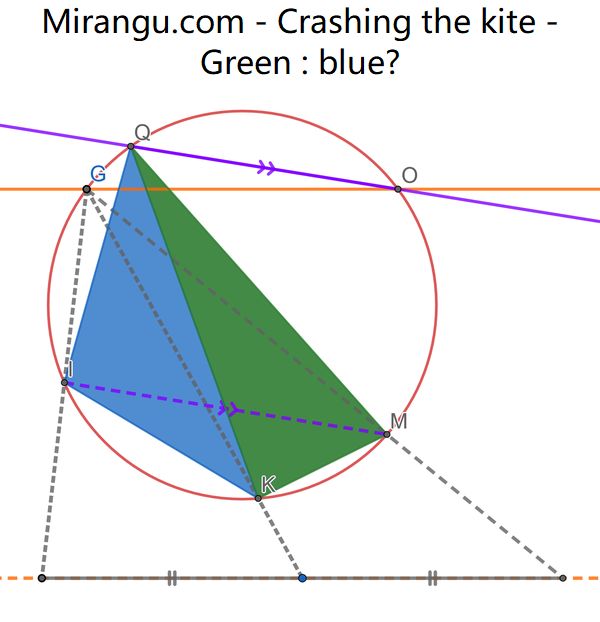
The orange lines are parallel, the purple lines are parallel, the dotted gray lines intersect the base at equal distances. What is the ratio of areas of the blue and green triangles?
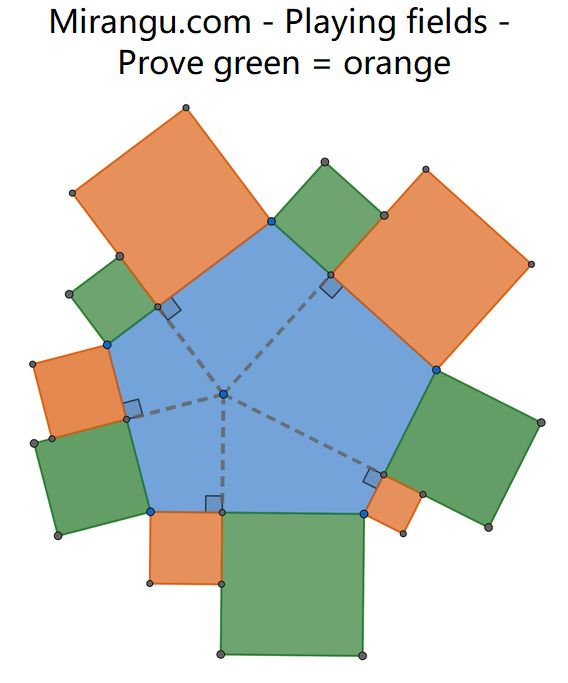
Show equality of the green and orange square playing field areas.
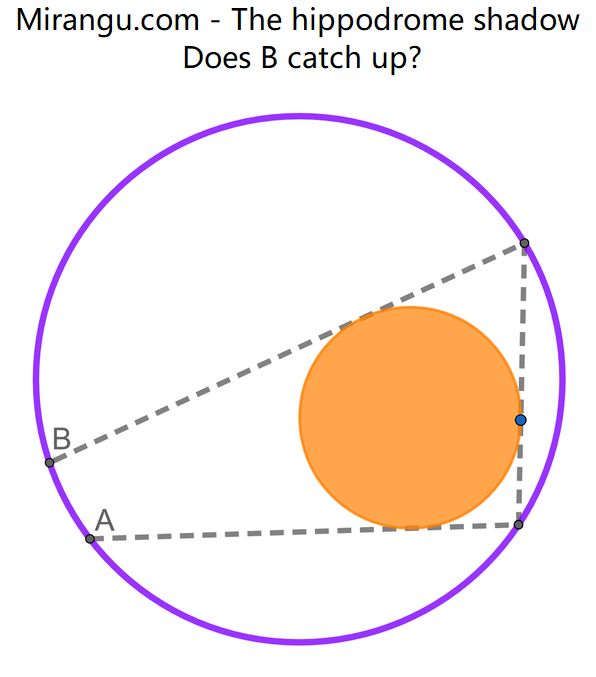
The racer at A is running counter-clockwise around the inside of the outer purple circle, with a “shadow racer” B following behind, related by the three chords that are tangent to the inner orange circle. Does the shadow B ever catch up with A?
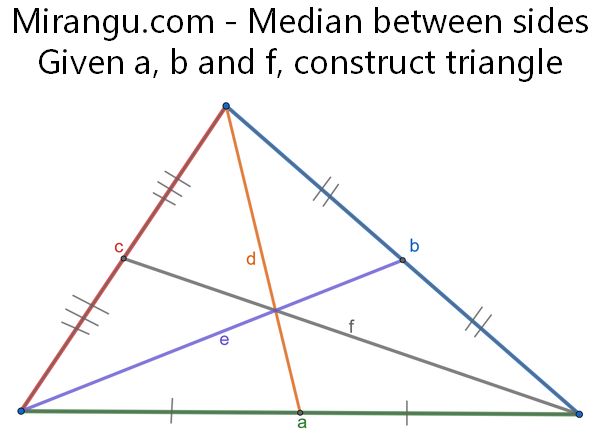
A triangle has sides a,b,c and the medians d,e,f ending at those sides, respectively. Given the lengths (a,b,f) construct the triangle. (Start with a triangle with side lengths determined in some manor from the given 3 lengths.)
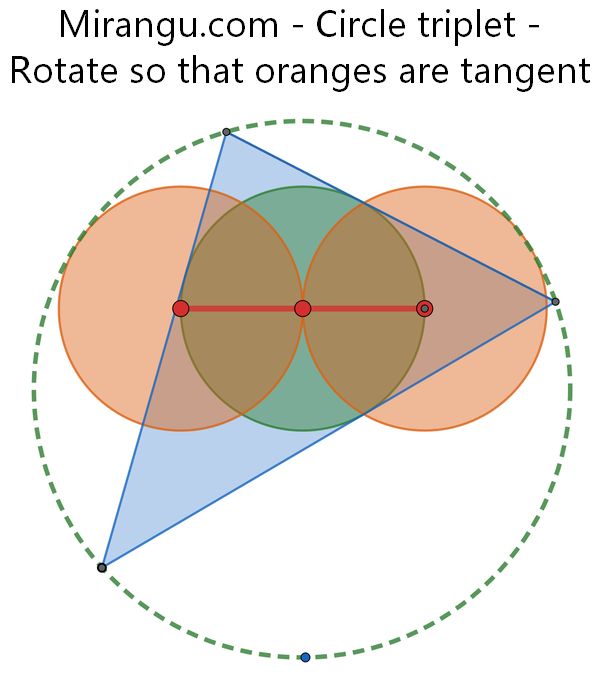
Identical circles have their centers aligned as shown, with the middle circle inscribed in a triangle. Show that the outer circles can be made tangent to the green circumcircle if the red axis is rotated correctly.
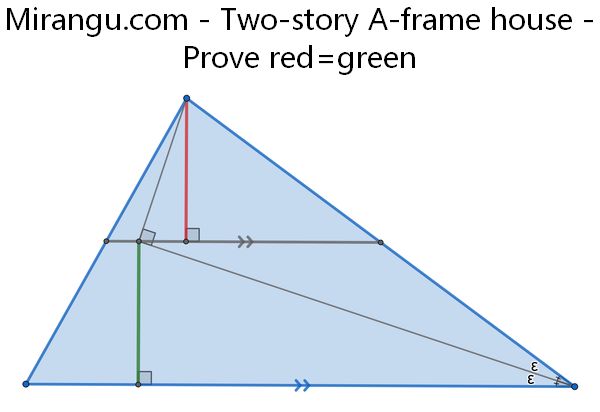
The slanted lines are perpendicular, and the one in the bottom story bisects the angle. Show that red equals green, so the stories have the same height.