The racer at A is running counter-clockwise around the inside of the outer purple circle, with a “shadow racer” B following behind, related by the three chords that are tangent to the inner orange circle. Does the shadow B ever catch up with A?
Scroll down for a solution to this problem.
Solution
No, B never catches up.
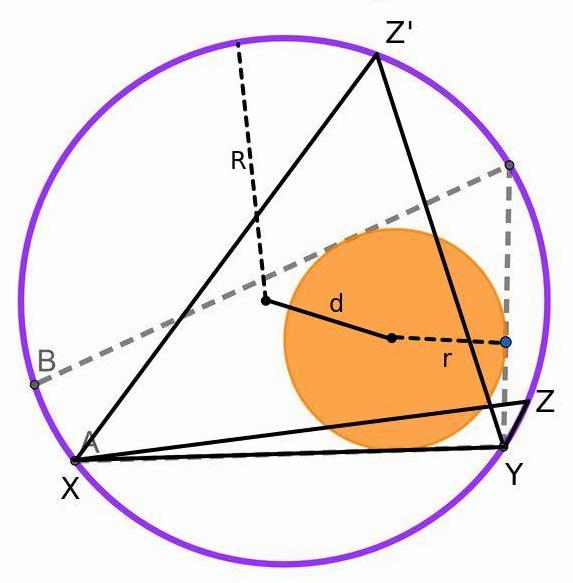
If B catches up, there is a triangle with inradius r, circumradius R, distance between centres d, so by Euler d² = R(R-r). But by continuity there is a triangle on XY with inradius r, so the incentre is also at distance d, but then the incircle is the same as the orange circle.
One reply on “The hippodrome shadow”
The answer is: A = B if and only if in the figure of M. Arcus R²-d² = 2Rr.
So A = B all the time or never!
This is the consequence of the theorem proved in the figure below.
See:
https://en.wikipedia.org/wiki/Modern_triangle_geometry#Poristic_triangles
with link [16]