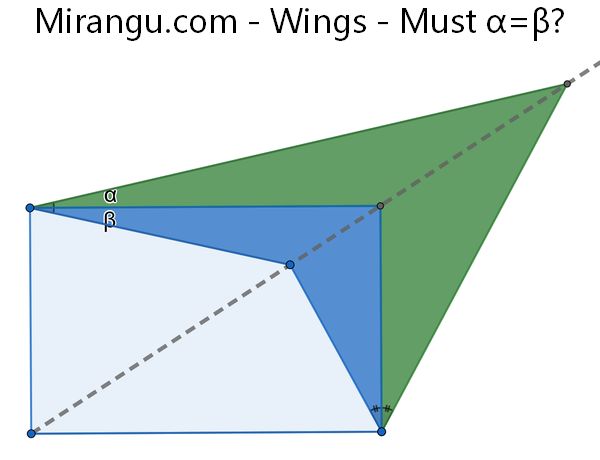
Two wings are attached to the corner of a rectangle, and have corners lined up with the diagonal of the rectangle. The angles at the lower wing tips are equal. Must α = β at the left wing tips?
Scroll down for a solution to this problem.
Solution
Yes, α = β.
Clearly equal if the rectangle is a square, then applying a horizontal stretch preserves equality of angles (measured against or perpendicular to direction of stretch anyway). Matthew Arcus
2 replies on “Wings”
Another solution, suggested by some, was to observe that the configuration of perpendicular lines bisecting another pair of lines, is *harmonic* (cross-ratio is -1), so when such a bundle of lines is intersected with a slanted line, you get a harmonic configuration of points along that line. Connecting that configuration of points to another point gives a harmonic bundle of lines through that point. If two lines of the bundle are perpendicular, as they are in this case, then those perpendicular lines are the two angle bisectors of the other two lines.
Another peculiarity with this one is the behavior of the tangents of angles.
Suppose t is the tangent of alpha (or beta), and u is the tangent of the common angle at the bottom right wing tip. Suppose that the rectangle is h times wider than it is tall. Then $\tan(t) = \tan(u)/h^2$.