The triangle ABC has orthocentre H, so that HA is an antenna above the green hill. The rectangle BCDE is inscribed in the circumcircle (ABC). Show that HA = CD = BE.
Scroll down for a solution to this problem.
Solution
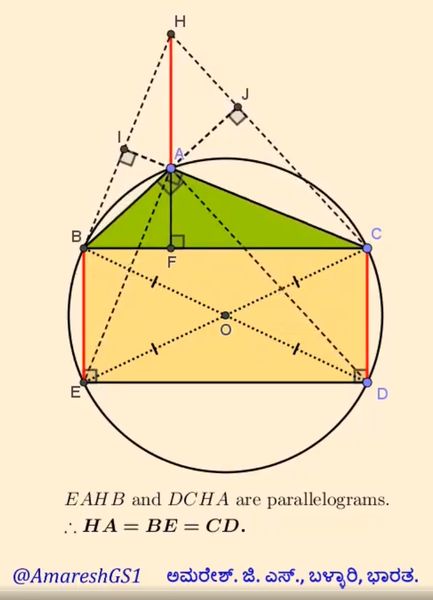
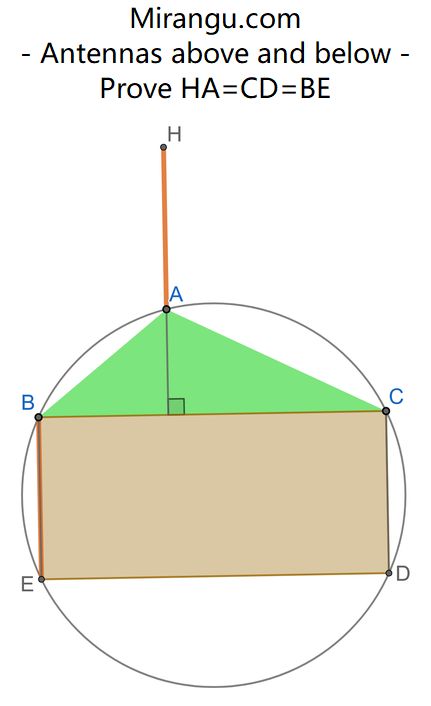
The triangle ABC has orthocentre H, so that HA is an antenna above the green hill. The rectangle BCDE is inscribed in the circumcircle (ABC). Show that HA = CD = BE.
Scroll down for a solution to this problem.

The triangle ABC has orthocentre H, so that HA is an antenna above the green hill. The rectangle BCDE is inscribed in the circumcircle (ABC). Show that HA = CD = BE. https://t.co/kOCreX0K8A By @MarshallWBuck pic.twitter.com/OwXHVtrQ84
— Mirangu (@Mirangu1) April 4, 2024
One reply on “Antennas above and below”
Let A, B, C denote (equal length) vectors from the center of the circle to those points. Then the vector sum A+B+C = H. (To show this we need to show that (H-A) is perpendicular to B-C, that H-C is perp to A-B, and that H-B is perp to A-C. But H-A = (A+B+C)-A = B+C, etc. So, we need to show that (A-B) is perp to A+B. But (A-B).(A+B) = A^2 – B^2 = |A|^2 – |B|^2 =0 because the vectors A, B, C all have the same length. Similarly, we show that (B-C).(B+C)=0 and (C-A).(C+A)=0.)
The antenna on the hill is represented by the vector H-A = B+C.
The vector of the “antenna in the ground” is B-E = B – (-C) = B+C.