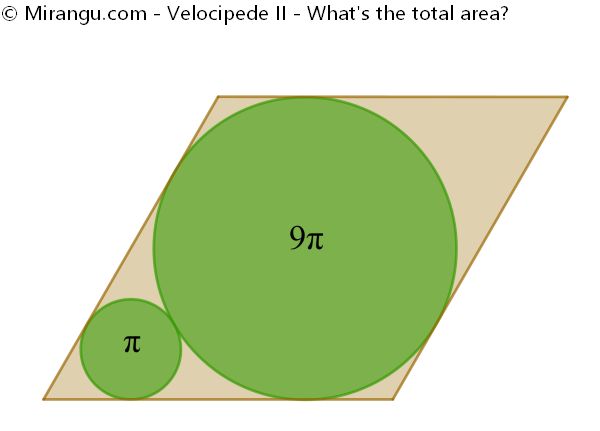
Two circles of area π and 9π respectively are contained in a parallelogram. What’s its area?
Scroll down for a solution to this problem.
Solution
The total area is 24√3.
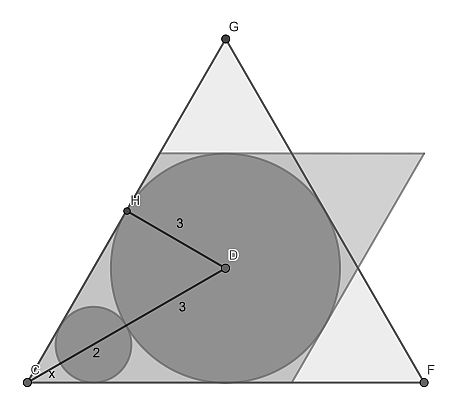
First proof that the lower left corner of the parallelogram is 60° (this was kindly provided by Galip). The line through the circle centres is its bisector. Consider right triangle CHD. From scale arguments it follows that x : 2 = x+2 : 6. It follows that x=1. This makes the sine of angle HCD equal to 1/2, hence it is 30°.
Completing the angles, it is seen that the parallelogram consists of two equilateral triangles of height h=6, each having an area of h2/√3.