Two congruent pyramids placed at different distances from the observer appear as equilateral triangles in a square frame. If the closest one is at 100 meter, how far is the distant pyramid?

Solution

The distance is 150√3 meter, which is approximately 260 m.

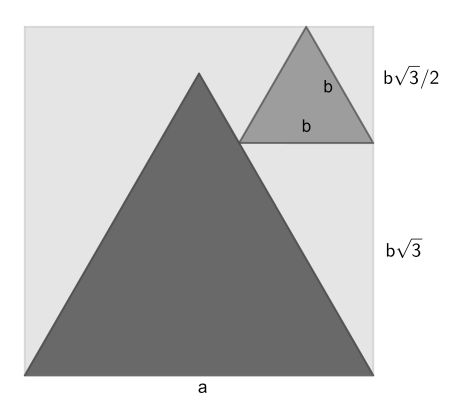
Using the two 30-60-90 triangles on the right side of the diagram, you can relate the square side a to the (apparent) small pyramid side b as a=b3√3/2.

Now it’s well known and easy to prove that the apparent size of an object is inversely proportional to its distance from the observer. Since it is given that both pyramids are of the same size, and the closest is at 100 meter, the other must be at 3√3/2 times 100 meters.