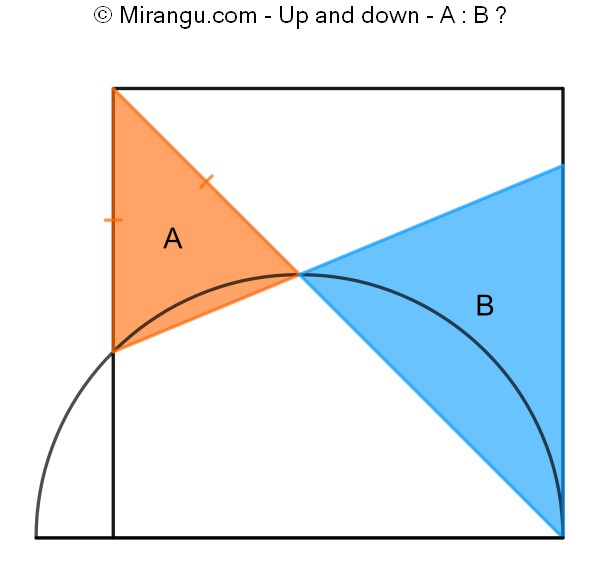
A semicircle and a square. Three secants and a tangent form two triangles. What is their area proportion?

Solution

The proportion A : B is 1 : 2.

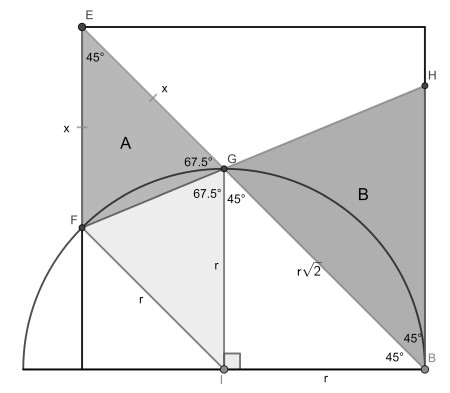
First it is easy to see that triangles EFG and BGH area similar, so to find their area proportion we only need to find the proportion of one of their sides and square it.

Name the length of the isosceles triangle EFG sides x. Constructing two other isosceles triangles in the semicircle IFG and IBG. The angles are easily found as shown.

Based on AAS, we see that IFG is congruent to EFG and hence x=r. Also, the side of BGH is r√2, so our required area proportion is (1/√2)²=1/2.