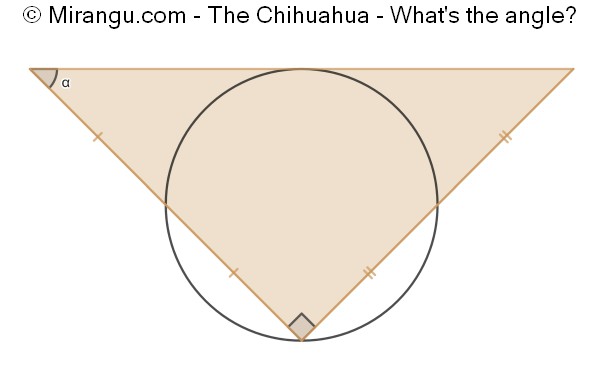
A circle and a right triangle. What’s the angle α?
Scroll down for a solution to this problem.
Solution
The angle α is 45°.
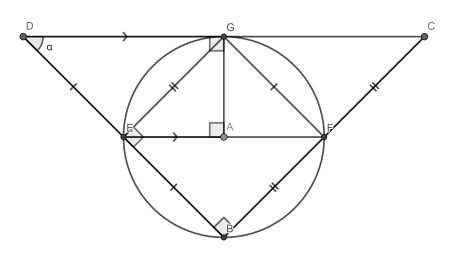
First, draw the line segment EF. From Thales we know it is a diagonal of the circle. From the midpoint theorem we also know it is parallel to DC and half its length. This enables us to basically fit three copies of triangle EFB on top of it as shown.
Now consider radius AG. Because DC is tangent, angle AGD is right. From the parallelness we infer also EAG is right. Therefore EFG is isosceles and since its top angle is 90°, the other two angles must be 45°. Triangle DGE is congruent, so this makes alpha is 45° as well.
Poem
I’m so small
And so kind
I like when you play with me
And go for some walks
I’m glad to stay with you
As for me you do
My heart is unselfish
And has only one wish
Just know you’re there
And for me you care
Still after your caresses longing
And for your love searching