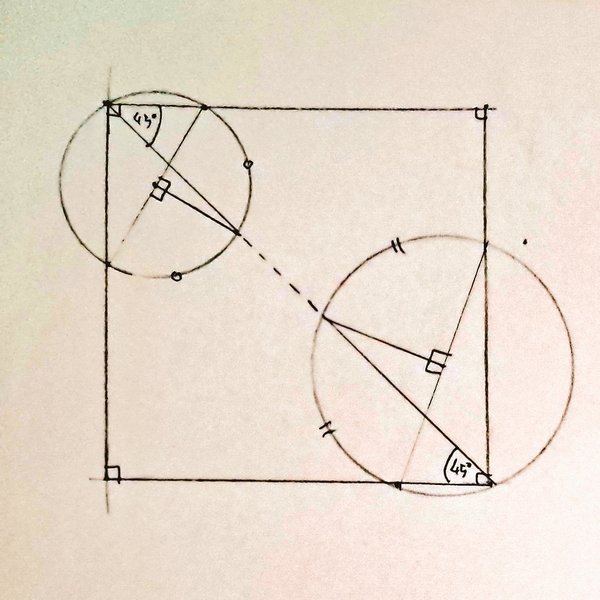
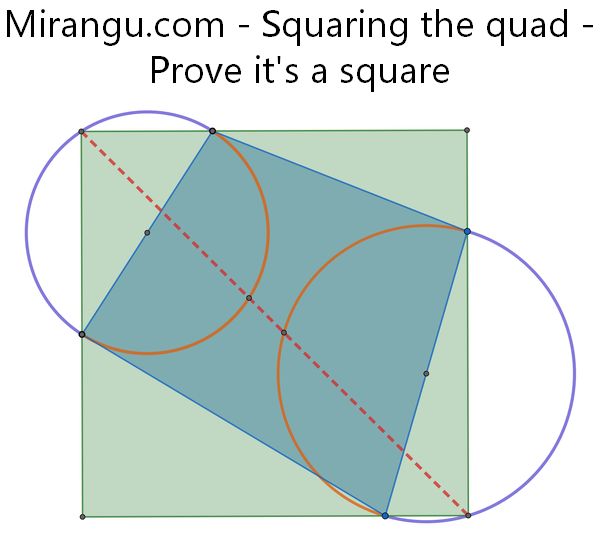
Form inward semicircles (orange) and outward semicircles (purple) on two opposite sides of a quadrilateral. Connect the midpoints of the orange arcs, intersecting with the purple arcs. Show that you obtain two corners of an enclosing square.
Scroll down for a solution to this problem.
Form inward (orange) and outward semicircles (purple) on two opposite sides of a quadrilateral. Connect the midpoints of the orange arcs, intersecting with the purple arcs. Show that you obtain two corners of an enclosing square. https://t.co/pShvWwfwdV By @MarshallWBuck pic.twitter.com/dVU8DHpR9M
— Mirangu (@Mirangu1) June 10, 2024
One reply on “Squaring the quad”
As pointed out by Lewis Corner, the construction produces a square but it does not necessarily contain the quadrilateral inside its boundaries. However each vertex of the quadrilateral will be on one of the lines extending one of the square’s sides.