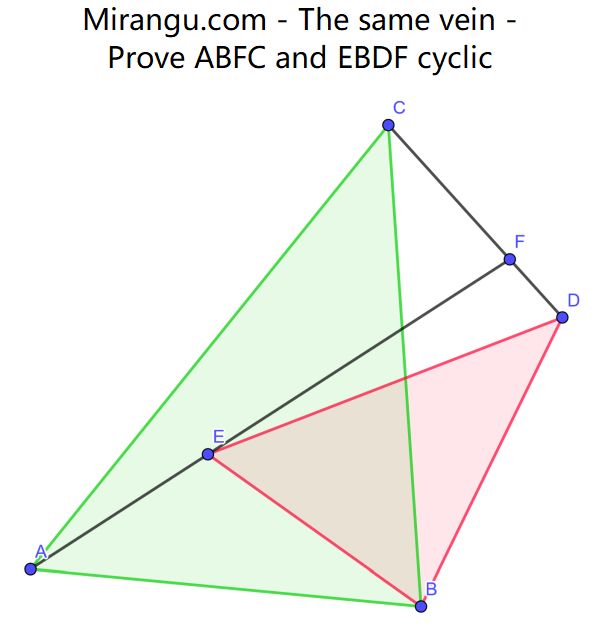
Two similar triangles ABC and EBD. Two line segments meet at point F. Prove that ABFC and EBDF are cyclic quadrilaterals.
Scroll down for a solution to this problem.
Solution
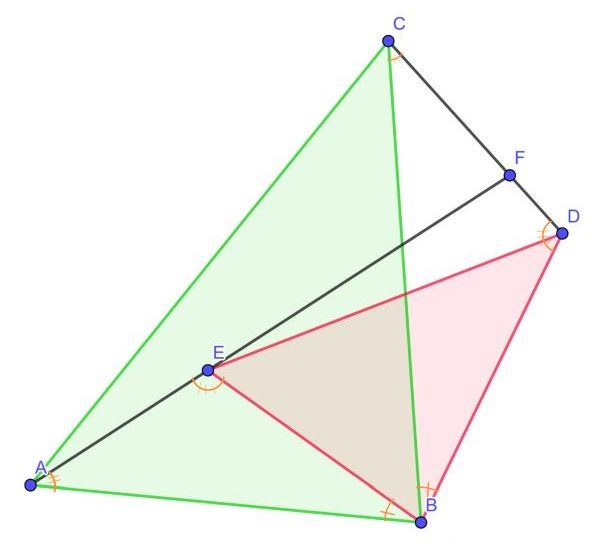
ΔABC∽ΔEBD
AB:BE=BC:BD
ΔABE∽ΔCBD
∠BAE=∠BCD, ABFC cyclic
∠AEB=∠CDB, EBDF cyclic