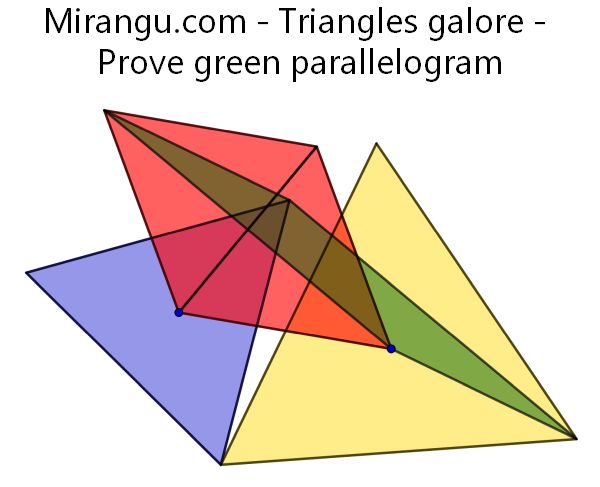
Four equilateral triangles. Two centres are shown. Prove that the green quadrilateral is a parallelogram.
Scroll down for a solution to this problem.
Solution
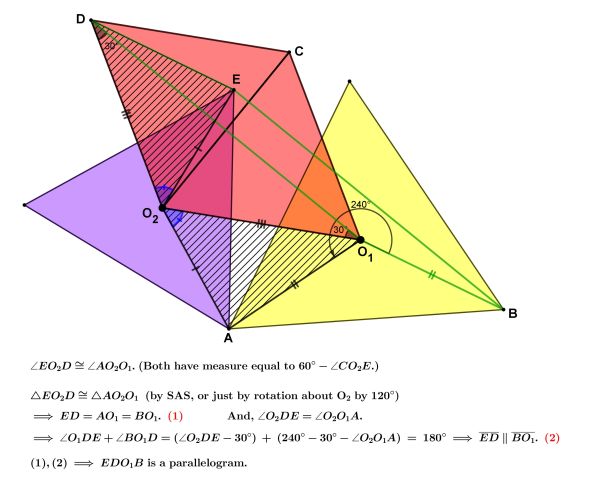
Solution by Marshall W. Buck:
Let w be the (complex number or linear transformation of 2-vectors) that rotates counterclockwise by 120 degrees. Put the purple/yellow common vertex at the vector (0,0)=0. Let b be the purple center vector, and c the yellow center vector.
Then the 4 corners of the green quadrilateral are as follows (clockwise from the highest point):
A=w(c-b)+b = (1-w)b+wc,
B=b + w(-b) = (1-w)b,
C=c + w(-c) = (1-w)c,
D=c.
Then A – B = wc, and D – C = wc, so A, B, C, D is a parallelogram.