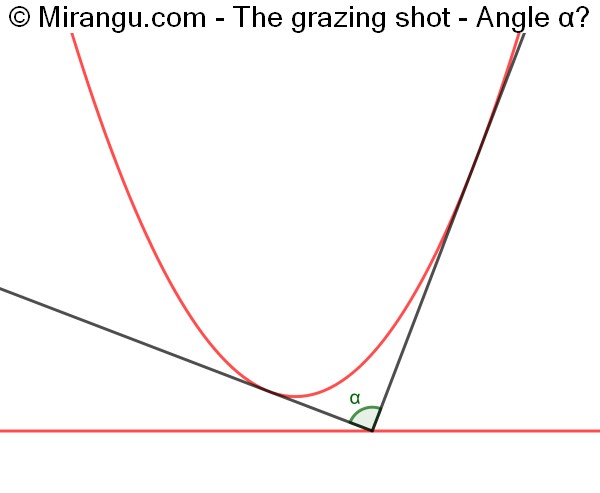
A parabola and its directrix in red. Two tangents intersect at a point on the directrix. What’s the angle α?
Scroll down for a solution to this problem.
Solution
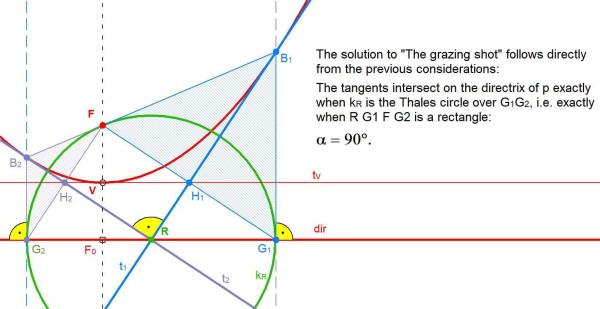
The angle α is 90°.
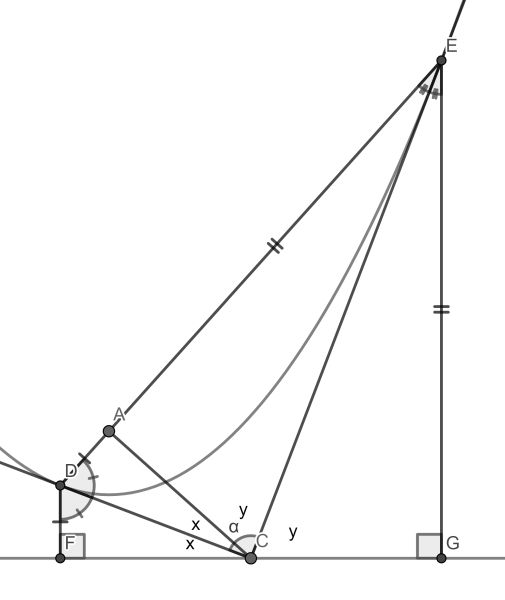
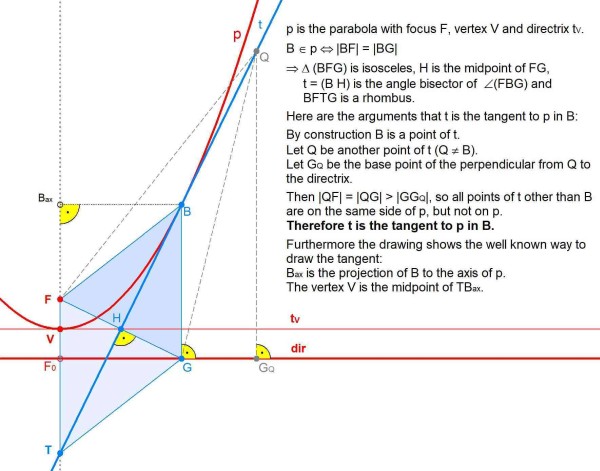
A is the focus point of the parabola. This solution uses two well-known facts:
- The distance of a point on the parabola to the focus is equal to that to the directrix.
- The tangent to a point on the parabola bisects the angle of the line segments from that point to the focus and to the directrix.
It then uses SAS to show congruence of triangles DCF and DCA and of triangles ECG and ECA. Finally, it follows from 2x+2y=180, that α=x+y=90.
Note that an interesting corollary is that angles DAC and CAE are right and thus DAE is straight.
Alternative solution
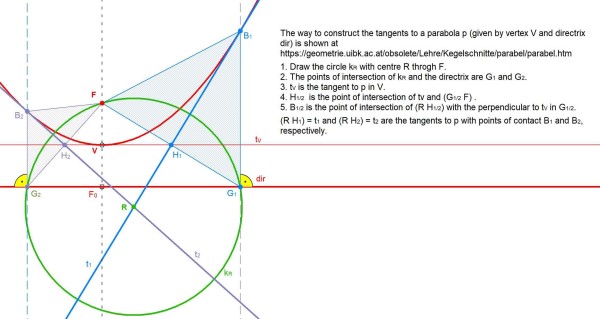
The below alternative solution was kindly provided by Peter H: Since geometry is less and less a topic in school, I have considered and presented the steps to the solution in more detail. Helpful was an old textbook (Lambacher Schweizer: Analytische Geometrie from 1958) and a website with animations for the constructions:
https://geometrie.uibk.ac.at/obsolete/Lehre/Kegelschnitte/parabel/parabel.htm