The apex of a parabola is the shared vertex of two rectangles. Proof that the rectangles are similar.
Scroll down for a solution to this problem.
Solution
Categories
Lopsided
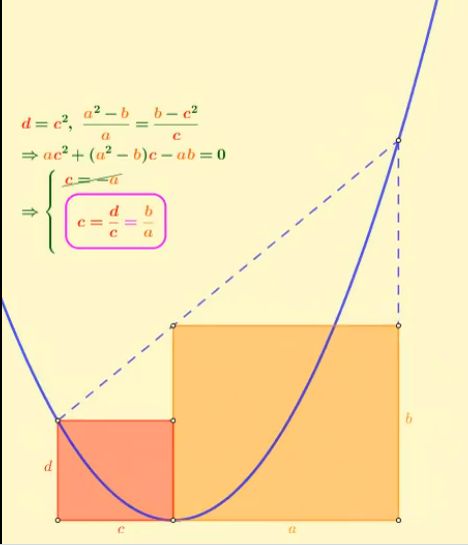
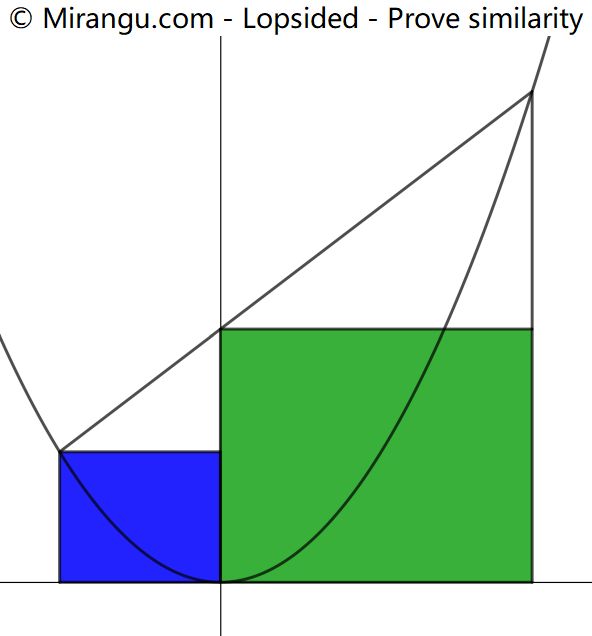
The apex of a parabola is the shared vertex of two rectangles. Proof that the rectangles are similar.
Scroll down for a solution to this problem.
One reply on “Lopsided”
A little more direct solution:
Slope of dotted line = (a^2-c^2)/(a+c) = a -c.
b = slope*c + d = (a-c)c + c^2 = ac.
Thus b/a = ac/a = c, and d/c = c^2/c = c, and rectangles have the same shape.