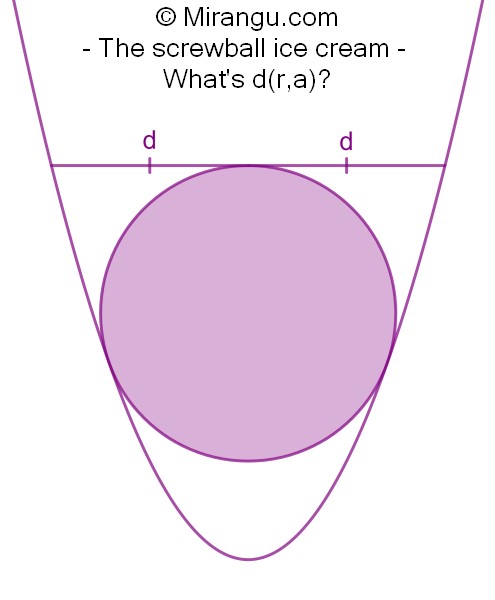
A circle of radius r touching both sides of a parabola having focal length a. A line segment tangent to the circle is split in two equal segments of length d. What is d in terms of r and a?

Solution

The segment length d=r+2a.

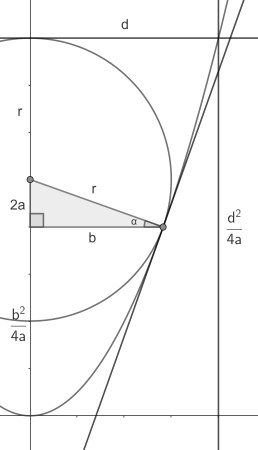
One can place the origin of a set of Cartesian coordinates in the parabola vertex and the y axis being it’s axis of symmetry. The parabola is then parametrised by y=x²/4a.

Naming the x-coordinate of the tangency point b, we can find the distances as shown above. We used the right triangle with constant height 2a, shown below.

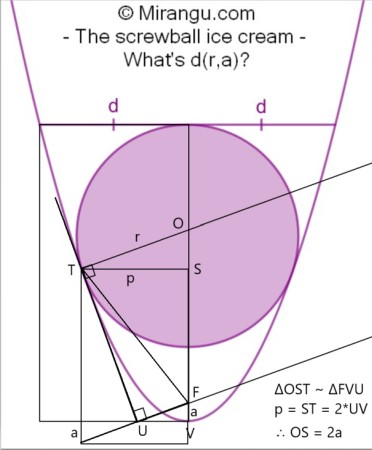
Applying the Pythagorean theorem in the triangle gives b²=r²-4a². Now equating the vertical sides of the rectangle gives d²/4a=b²/4a+2a+r. Eliminating b from these two equations gives d=r+2a.

Poem

I scream
Ice cream can be sticky
Screwball ice cream can be sweet
To eat, to hold and melt, it’s funny
I eat it always when it’s sunny
So much choice, and flavours so many
With crushed nuts juice and Tasty sprinkles candy
Ice cream is my weakness,
It makes me glad and lucky

Bella