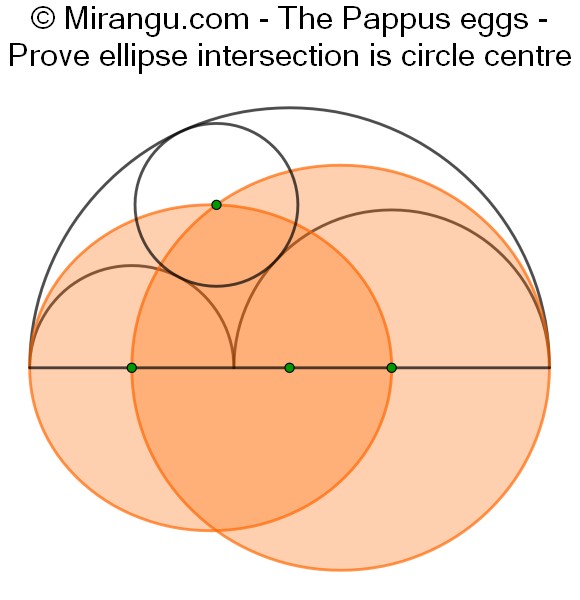
Three semicircles and a circle with their centres. Two orange ellipses with focal points in the semicircle centres (they share the middle one). Prove that their upper intersection point coincides with the circle centre.
Scroll down for a solution to this problem.
Solution
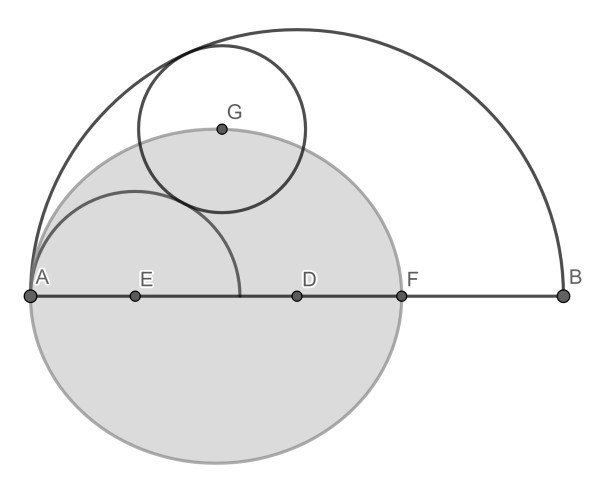
The prove is basically a corollary of the previous puzzle. Consider the left ellipse. The sum of the distances to the ellipse focal points E and D must be constant. We know from the previous puzzle that EG+DG=EA+DB. But DB=DA, so both A and G lie on the ellipse. Of course, since the inner right semicircle also touches both the outer and inner left one, its centre F is also in the ellipse.
The reasoning for the right ellipse is analogous, so G must be on both ellipses and thus coincides with their intersection.
Poem
The egg or the chicken
Who came first ?
Some say the egg
Others the hen
Who holds the truth?
All we know
Some come from eggs
An egg can be so small
Or very big and tall
We look in the henhouse
When we are hungry
And cook them hardboiled
Or even crunchy
We like them all