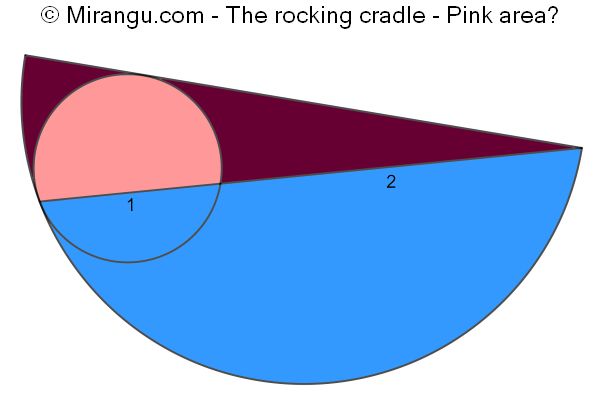
A semicircle and an interior circle are tangent to each other. The chord towards the tangency point is divided in segments of length 1 and 2. What is the pink area?
Scroll down for a solution to this problem.
Solution
The pink area is (2-√3)(7π+3)/12, which is approximately 0,56.
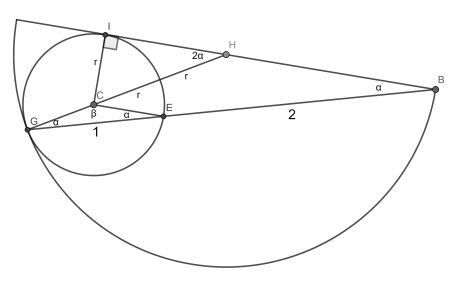
The proof starts by using the fact that for interior touching circles, radii and chords are aligned. Therefore triangles GCE and GHB are similar and have length proportion 1 : 2. Thus the semicircle has three times the radius of the circle.
Now from the Inscribed angle theorem and from sin(2α)=1/2, we find that 2α=30°. Therefore β=150°.
Focussing on triangle GCE, it is straightforward to find that r=1/(2sin(75)). The pink area is a circular sector of 210° plus triangle GCE, which amounts to r2(21π/36+sin(150)/2). This can be worked out to the expression above.
Poems
The sleeping baby
So tender in the night
The parents are caring
Suddenly a bird is twittering
A nice song
I remember my childhood
Flashback to my past
My mother the cradle rocking
And sorrows comforting
And a gently rocking cradle for a peaceful resting.
Day after day
Is coming the night.
While bells are ringing,
We’re on time and fight
Every day
Life is so good
But do run to fast.
While it’s so stunning,
Expect the forecast:
Sky will be good.