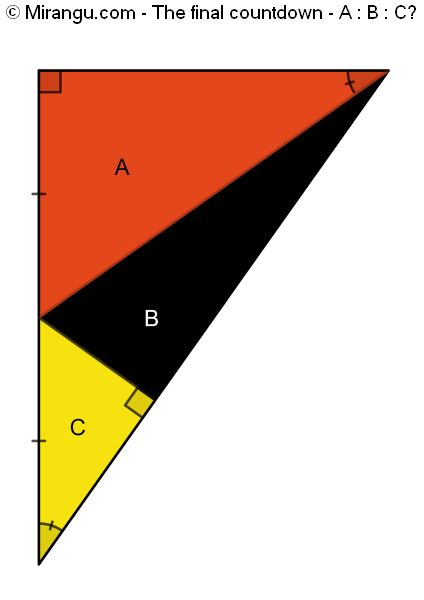
A right triangle is divided in three right triangles. What is the area proportion A : B : C?
Scroll down for a solution to this problem.
Solution
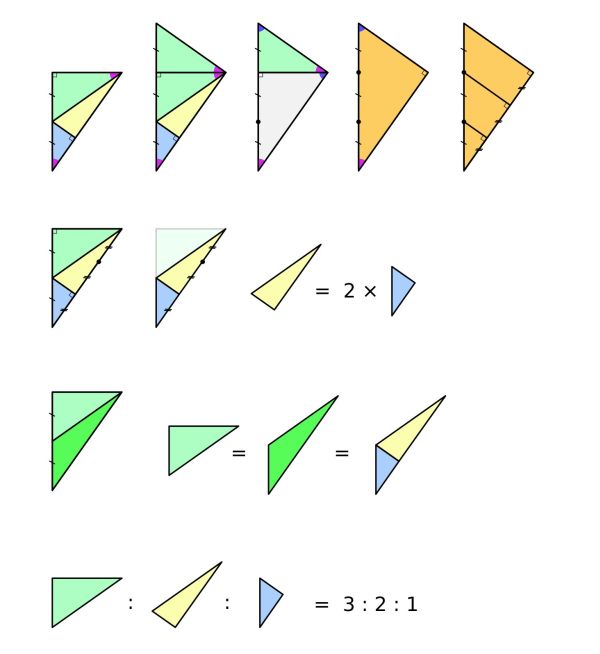
The areas have proportion 3 : 2 : 1.
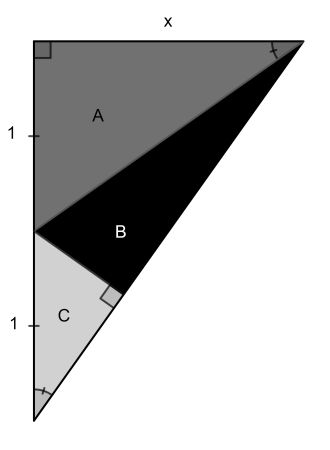
This solution starts by setting the equal line segments to length 1. From similarity of triangle A to the whole triangle we get 1/x=x/2, so x=√2.
Therefore similar triangles A and C have side proportion 1 : √2 : √3. The hypothenuse of C is 1, therefore we get for the areas A=3C.
Since the combined triangle B+C has the same area as A (same base and height), it follows that B=2C.
Visual solution