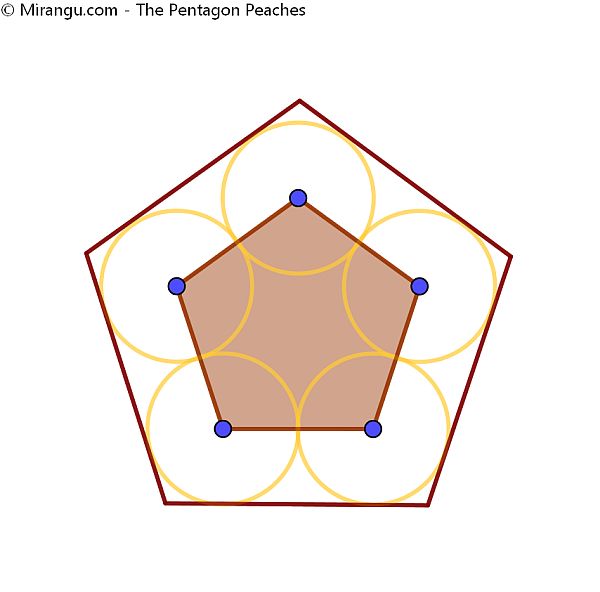
Five equally sized peaches are closely packed in a pentagon-shaped box. Their midpoints are the vertices of a smaller pentagon. What fraction is shaded?

Solution

The shaded fraction is 1/(1+tan(36))², which is approximately 0,335.

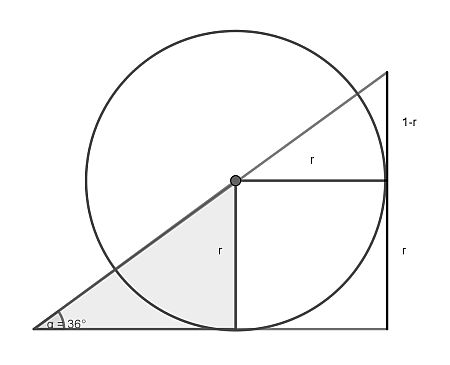
The problem can be solved by looking at the right triangle representing half of a sector of the pentagon, that is copied ten times around. Its angle at the center measures 36 degrees.

Set the length of the right side to 1 and draw two of the circle radii as shown. Now from similarity of the right triangle in the top right corner to the whole, it follows that tan(36)=(1-r)/r. So r=1/(1+tan(36)).

So the edge of the inner pentagon is r times that of the outer and the proportion of their areas is r².