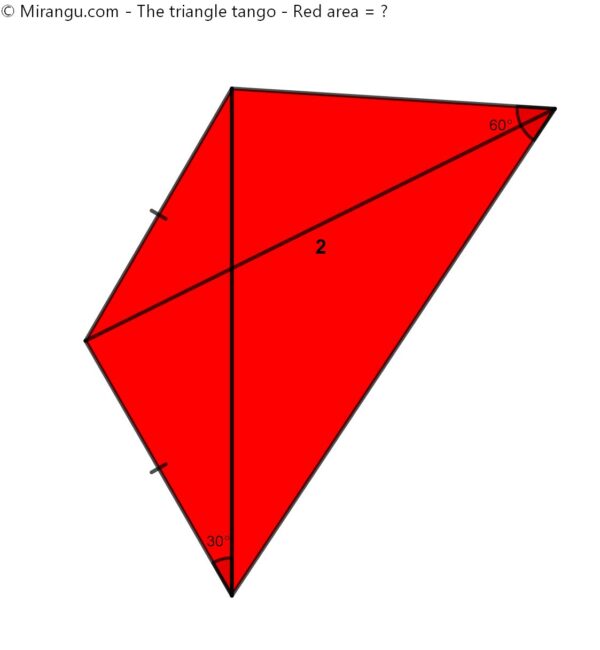
An isosceles triangle is attached to another triangle with a 60-degree angle as shown. Their opposite vertices are connected by a line segment of length 2. What is the area of the quadrilateral?
Scroll down for a solution to this problem.
Solution
The red area is √3.
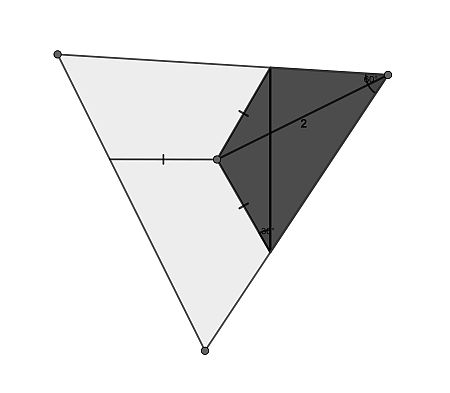
By using the interior angle sum, it is easily seen that the quadrilateral can be copied twice and arranged so that the three congruent quadrilaterals exactly form an equilateral triangle. The line segment of length 2 connects a corner to its centre.
Now in an equilateral triangle, this distance is two thirds of the height, which in turn equals √3/2 times the base. Therefore the area of the quadrilateral , being one third of the total, can be calculated from this segment length.