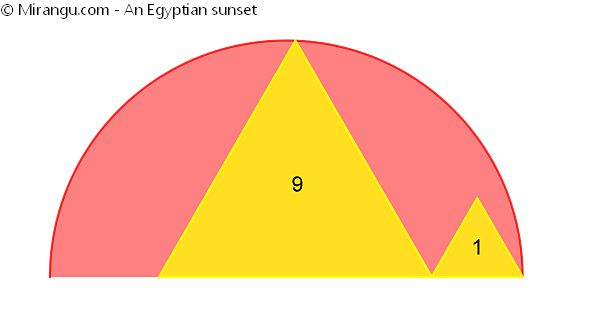
A semicircle touches a large equilateral triangle (area equals 9) at its apex and a smaller adjacent equilateral triangle (area equals 1) at its base as shown. What is the total red area?
Scroll down for a solution to this problem.
Solution
The total red area is 338π/(25√3) – 10, which is approximately 14,52.
Suppose the base of the unit triangle is a. From the area of an equilateral triangle you it follows that a2 =4/√3. The base of the large triangle is 3a since its surface is 9.
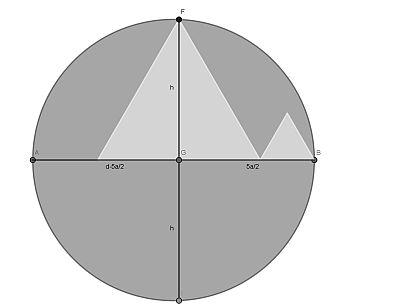
Now draw the altitude of the large triangle. Its length h=3a√3/2. Mirror the semicircle and extend the altitude. This line segment of length 2h divides the diameter in two parts of length d-5a/2 and 5a/2.
The crucial step is to apply the Intersecting Chords Theorem: h2=5a/2 x (d-5a/2). Solving for d gives d=26a/5, which in turn gives a radius of 13a/5. The requested area is πr2/2-10.