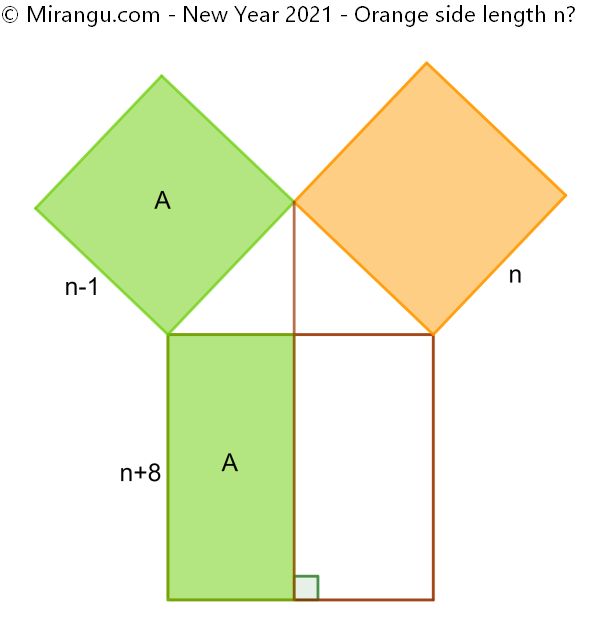
Three squares are placed as shown. Given that the green areas are equal, what is the side length of the orange square?
Scroll down for a solution to this problem.
Solution
The answer is n=21.
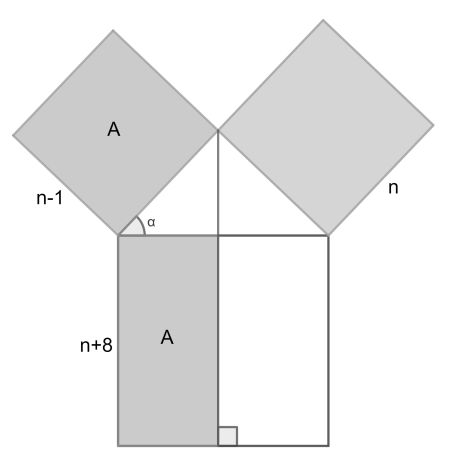
Naming the angle between the small and the large square α, we can deduce from the equality of areas: cosα=(n-1)/(n+8).
Now we apply the cosine rule in the triangle: n2=(n-1)2+(n+8)2-2(n-1)(n+8)cosα. Getting rid of the cosα, we get n2-18n-63=0. This quadratic equation has only one positive root: 21.
Poem
Geometrical poet Belladonna started the new year thus:
Les voeux de l’année 2021
Inclus dans trois carrés
Des cartes vertes et oranges
Portant des messages
Des voeux , des louanges ,
Des messages écrits
D’espoir, d’amour de poésie ,
Dire l ‘existentiel
Dire ce qui est essentiel
Bella