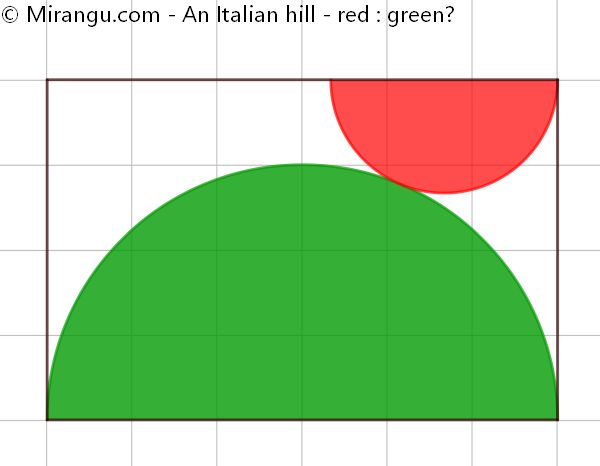
Two semicircles inside a rectangle. What is the proportion of the red to the green area?
Scroll down for a solution to this problem.
Solution
The area red : green is 16 : 81.

We have named the green radius R and the red one r. Then we draw both the line segment connecting the circle centres and the altitude. From the Pythagorean theorem we find that h2=(R+r)2-(R-r)2=4Rr.
This can be rewritten as r/R=(h/2R)2. Now h and 2R are height and width of the rectangle respectively. So r/R=(4/6)2. The requested area proportion is the square of this: (2/3)4=16/81.
Poem
Geometrical poet Belladonna had another association with this puzzle:
C’est vrai ce sont les couleurs de l’Italie
Mais la comparaison s’arrête ici
La planète verte entre en collision
Avec le soleil rouge en fusion
Les 2 planètes sont choquées
Elles ont un peu trop fêté
2021, la nouvelle année !
Belladonna