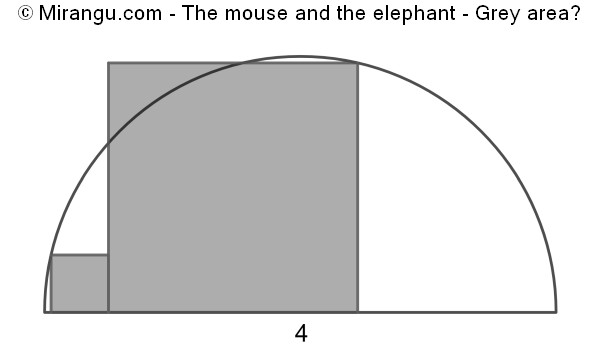
Two squares and a semicircle of diameter 4. What is the total square area?
Scroll down for a solution to this problem.
Solution
The total square area is 4.
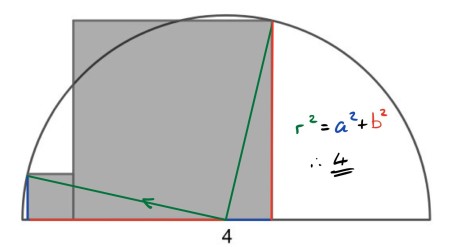
This solution takes a point on the diameter that is the left square side (a) to the left of the lower right vertex of the right square. From this point two right triangles can be constructed which, by comparing sides a and b and using SAS, are seen to be congruent.
So this point is equidistant from the circle circumference and on diameter and therefore1The point is the intersection of the perpendicular bisector of the two circumference points and the diameter, and therefore it is unique. must be the circle centre. Using the Pythagorean theorem, one can calculate the sum of the square areas.
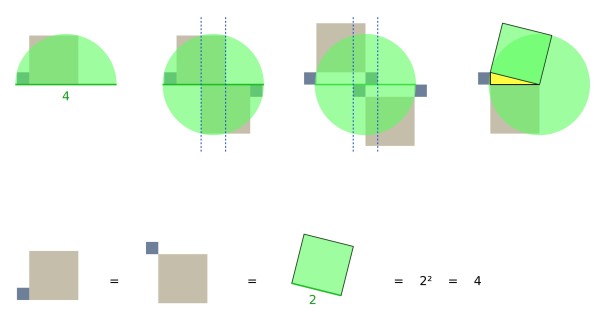
Please find here a beautiful animated solution including all possible configurations by Per Henrik Christiansen.
Visual solution
Poem
The elephant and the mouse
In this small house
The 2 went to a race
To see who would take the 1st place
The elephant was big and scared
The mouse small and well prepared
The race begun
What a fun !
The elephant hidden behind a tree so easy
So nice to see
The mouse won easily