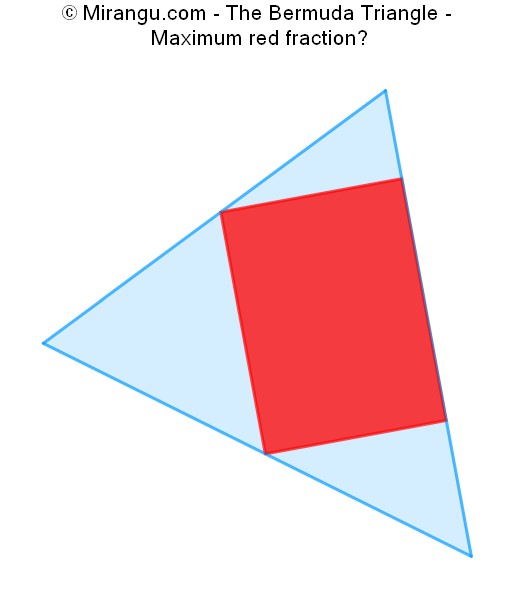
A triangle with an inscribed rectangle. What is the maximum red fraction?
Scroll down for a solution to this problem.
Solution
The maximum rectangle fraction is 1/2.
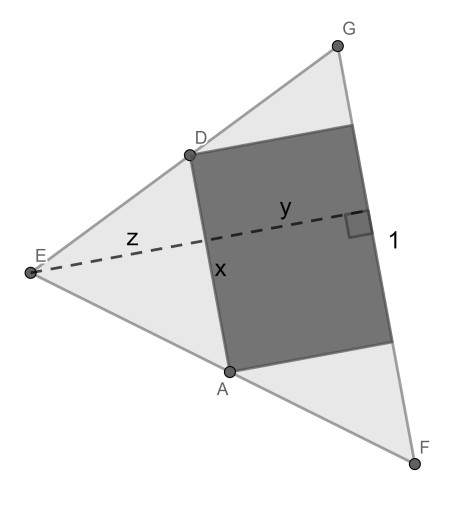
We scale the base FG of the rectangle to 1. Name the rectangle height x and its width y. Note that x lies between 0 and 1. Now it is trivial that triangle EAD is similar to EFG. Name its height z. From this similarity we get z/x=(z+y)/1, leading to z=xy/(1-x).
The rectangle area is xy, whereas the total area is (y+z)/2=y/(2(1-x)). The fraction is f(x)=2x(1-x). Note that it does only depend on x, because y has cancelled out. This formula can be graphed as an upside down parabola with its maximum of 1/2 at x=1/2.
Poem
The Bermuda triangle
From Florida to Bahamas and Porto Rico
A place to see, a sea to go
It’s the true reality
For our back door and the sea mystery
Some boats shipwrecked even from the army
The deadly triangle
The myth remains, completely
With ships and skeletons, maybe !!