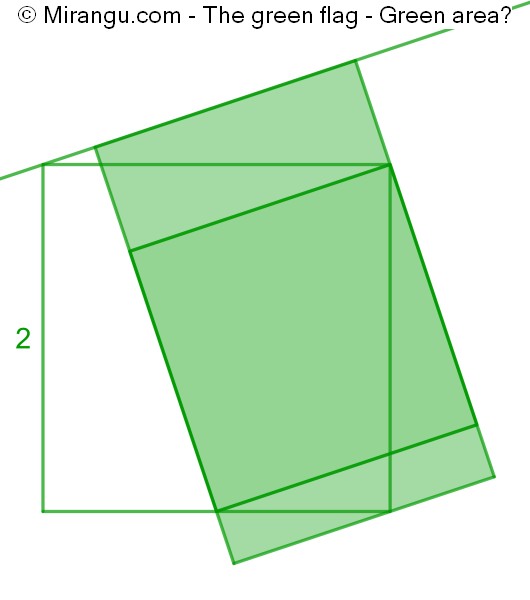
A square of side length 2 shares a vertex with another square that is elongated to form a green rectangle. What is the rectangle area?
Scroll down for a solution to this problem.
Solution
The rectangle area is 4.
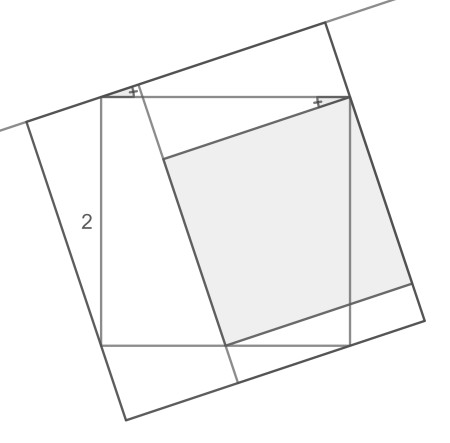
The puzzle can be transformed to one with three concentric inscribed squares, two of which are parallel. The outer square can easily be discerned. The inner square just needs to be translated horizontally to the left until it fits. Note that, since it fits vertically already, rotational symmetry implies it will also fit horizontally. Here is a nice animation of this transformation by G.S. Amaresh.
Now the relative sides of inscribed concentric squares have a proportion C that depends only on their relative angle1Calling the relative angle α, the side proportion constant is easily calculated as C(α)=cos(α)+sin(α).. It follows from the parallel lines of the rectangle that the inner square inside the middle square has the same relative angle as the middle square in the outer square. Since the rectangle area is the product of the inner square side 2/C with the outer side 2*C, the proportionality constants will cancel. The rectangle therefore has the same area as the middle square.
Poem
A green flag for a the Earth
A permission to go and do
Just a sign of approval
The opposite is a red flag
Concerning warning for traits in people, games or jobs for you
Just a sign of bad potential
Green could be for hope and renewal
Or safety in drugs and medical