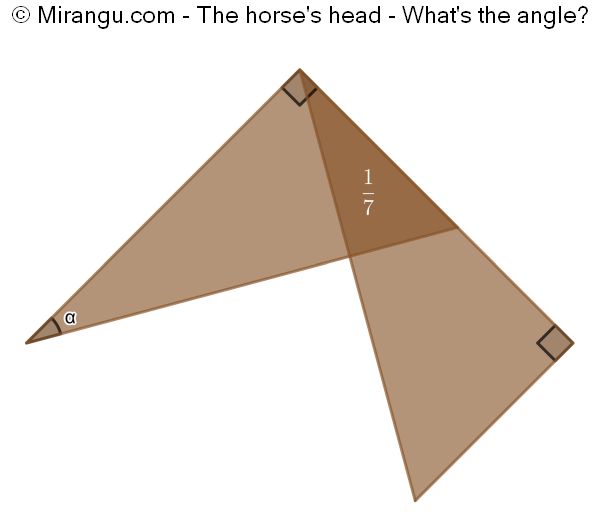
Two congruent right triangles share a vertex. If the overlap represents 1/7 of the total area, what’s the angle?
Scroll down for a solution to this problem.
Solution
The angle α=30°.
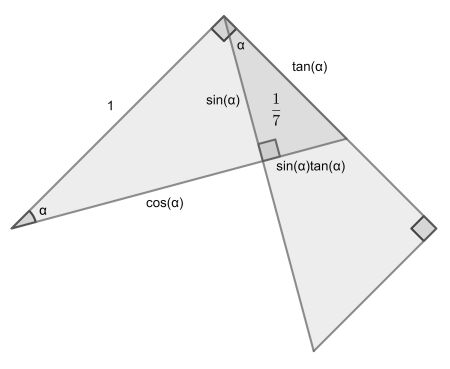
Because of angle comparison we find that the overlap triangle is similar to the two large ones. We can then place the lengths as shown.
Now the overlap area is sin2(α)tan(α)/2. The total area is two times the area tan(α)/2 minus the overlap. The fraction is easily worked out as sin2(α)/(2-sin2(α)).
Setting this fraction to 1/7, we find sin2(α)=1/4 and since α is acute we find sin(α)=1/2 and hence α=30°.
Poem
The horse’s head is inspiring
The horse whisperer is talking
To his best friend
A mustang strong and loving
The horse is understanding.
Everyday early in the morning
The whisperer and the horse are practising
And that’s why love between horse and man is beginning