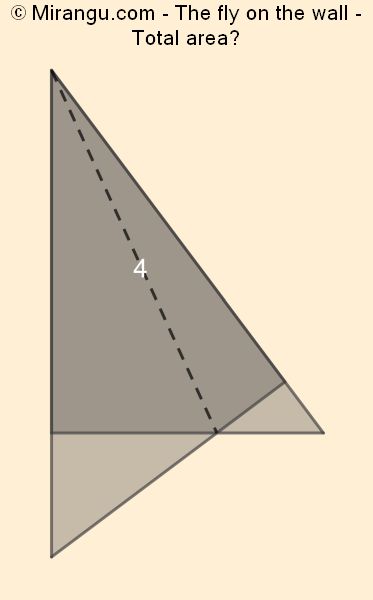
Two similar but not necessarily congruent 3:4:5 triangles are placed such that their smallest angles overlap. The line segment connecting the common vertex to the small side intersection point has length 4. What is the total area?

Solution

The total area is 6.

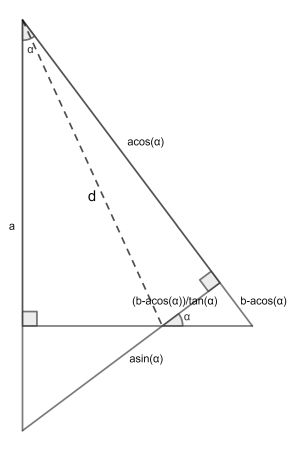
We will deduce a formula for two arbitrary similar right triangles placed as prescribed. Name their overlapping angle α and their respective hypotenuses a and b. Using similarity of the little triangle in the lower right corner to the big ones, we can easily fill in some lengths as shown.

The total area is the sum of the triangle with hypotenuse a and the little one: A=a²cos(α)sin(α)/2+(b-acos(α))²/(2tan(α)). This is worked out as A=(a²+b²-2abcos(α))/(2tan(α)).

Now using the Pythagorean theorem in the right triangle of which d is the hypotenuse, we get d²=a²cos²(α)+((b-acos(α))/tan(α))²=(a²+b²-2abcos(α))/tan²(α).

Combining the two equations we arrive at A=d²tan(α)/2. In our special case d=4 and tan(α)=3/4, leading to A=6.

Please find here an animated version of this generalised result by uila.