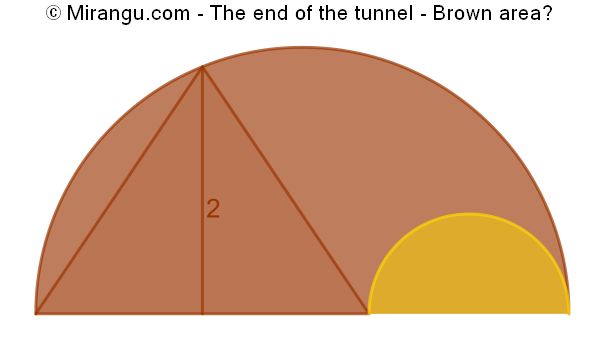
Two semicircles and two congruent triangles with a side of length 2. What’s the brown area?
Scroll down for a solution to this problem.
Solution
The brown area is 2π.
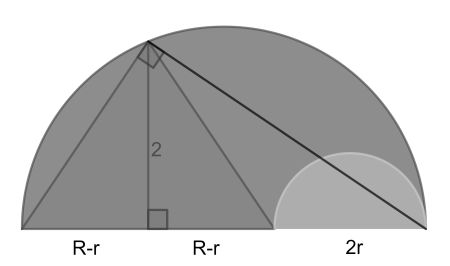
Naming the radius of the large semicircle R and the small one r, and using similarity of the triangles, the lengths as shown can easily be found. Using Thales, we can also draw two right angles as shown.
Now a larger similar triangle is formed with sides 2 and R+r. Similarity gives 2/(R+r)=(R-r)/2, leading to R2-r2=4. The brown area is (R2-r2)π/2.
Poem
We are in a tunnel
But the light is at the end of the passage
Like the allegory of Plato’s cavern
Giving names to the shadows
This is not the real world
We are still in prison
In our sad reality and trapped in ignorance
But the light is coming
And wisdom for our souls .